Height and Distance
This is the application of trigonometry which helps us to find the height of any object and the distance of that object from any point.
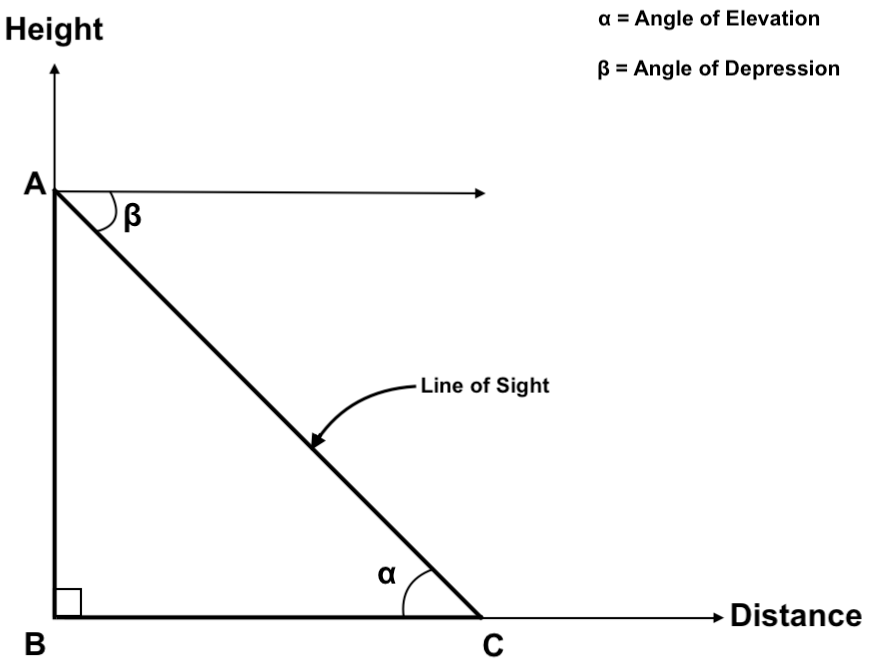
Line of Sight
A line of sight is the line which is drawn from the eye of an observer to the point where the object is viewed by the observer.

Horizontal Line
A horizontal line is the line which is parallel to ground level.
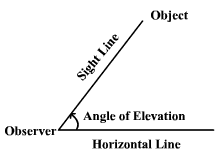
Angle of Elevation
If the object is above the horizontal line and we see the object from the eye, then an angle which is formed by the line of sight with the horizontal line is called angle of elevation.
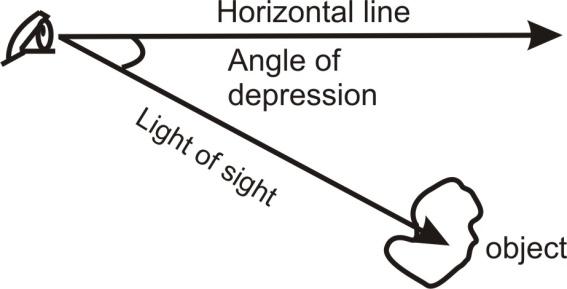
Angle of Depression
If the object is below the horizontal line and we see the object from the eye, then an angle which is formed by the line of sight with the horizontal line is called angle of depression.
Example- The shadow of a building standing on a level ground is found to be 40 m longer when the Sun's altitude becomes 30° from 45°. Find the height of the tower.
Solution:-

Solution:- given, PQ = 40 m, ∠ SPR = 30° and ∠ SQR = 45°
Let the height of the tower be x m.
In triangle SQR,
tan 45° = SR/QR
or, 1 = x/QR
or, QR = x ………(1)
In triangle SPR,
tan 30° = SR/PR
or, 1 / √3 = x /( PQ + QR )
or, 1 / √3 = x /( 40 + x )
or, 1 / √3 × ( 40 + x) = x
or, 40 + x = √3x
or, √3x - x = 40
or, x ( √3 - 1 ) = 40
or, x = 40 / ( √3 - 1 )
or, x = 40 / ( 1.732 - 1 )
or, x = 40 / 0.732 = 54.644
∴ Height of tower = 54.64 m
Example- The angles of elevation of the top of a tower from two points which are at distances of 16 m and 4 m from the base of the tower and in the same straight line with it are complementary. Find the height of the tower.
Solution:-
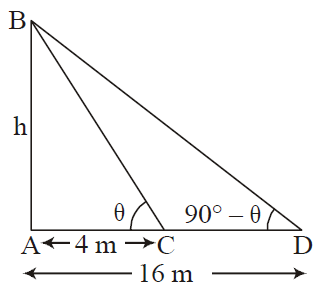
given, angles are complementary.
Let the height of the tower be h m.
In triangle BAC,
tanθ = BA/AC = h/4 …………(1)
In triangle BAD,
tan( 90° - θ ) = BA/AD
or, cotθ = h/16 ………………(2)
On multiplying Eq. (1) and (2), we get
tanθ × cotθ = ( h/4 ) × ( h/16 )
or, 1 = h2 / 64
or, h2 = 64
or, h = √64
∴ Height of the tower = 8 m
Example- What is the angle of elevation of the Sun when the shadow of a pole is √3 times the length of the pole?
Solution:-
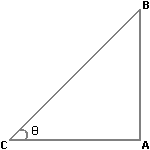
Let the length of the pole be x m. Then
Length of shadow = √3x
In triangle BCA,
tanθ = BA/AC
or, tanθ = x / √3x
or, tanθ = 1 / √3
or, tanθ = tan 30°
∴ θ = 30°