Height and Distance
- If a flag staff of 6 m height placed on the top of a tower throws a shadow of 2 √3 m along the ground, then the angle that the sun makes with the ground is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, OP be the tower of height h m and PQ be the flagstaff of height 6m. Let, the sun make an angle θ with the ground. Let, OA = x and AB = 2 √3 be the shadows of the tower and the flagstaff, respectively.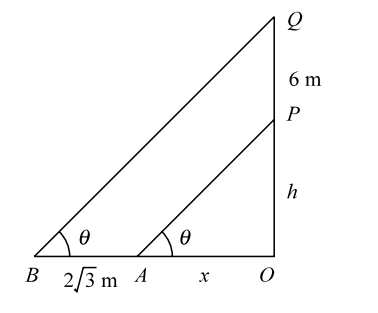
Correct Option: A
Let us draw the figure from the given question.
Let, OP be the tower of height h m and PQ be the flagstaff of height 6m. Let, the sun make an angle θ with the ground. Let, OA = x and AB = 2 √3 be the shadows of the tower and the flagstaff, respectively.In triangle OAP , tanθ = OP OA ⇒ tanθ = h ............ ( 1 ) x Also, In triangle OBQ , tanθ = OQ OB ⇒ h + 6 = tanθ ............ ( 2 ) x + 2√3
From equations ( 1 ) and ( 2 ) , we get∴ h = h + 6 ⇒ hx + 2√3 h = hx + 6x x x + 2√3 ⇒ 2√3h = 6x ⇒ h = 6 = √3 x 2√3 ⇒ tan θ = √3 = tan60° ⇒ θ = 60° . 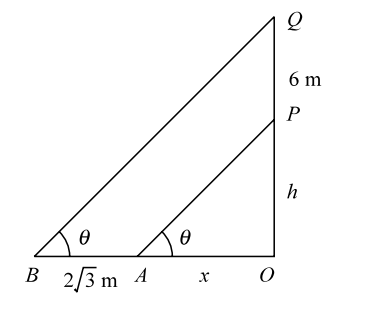
- A man is standing on the 8 m long shadow of a 6 m long pole. If the length of the shadow is 2.4 meter, then the height of the man is :
-
View Hint View Answer Discuss in Forum
As per the details of given above question , we have
Let, h be the height of the man.
Given :- The length of the shadow = 2.4 m
The length of the shadow of the pole = 8 m and the height of the pole = 6 mCorrect Option: C
As per the details of given above question , we have
Let, h be the height of the man.
Given :- The length of the shadow of the man = 2.4 m
The length of the shadow of the pole = 8 m and the height of the pole = 6 m∴ height of the pole = height of the man shadow of the pole shadow of the man ⇒ 6 = h ⇒ h = 3 ( 2.4 ) = 1.8 m. 8 2.4 4
- The angle of elevation of the top of a TV tower from three points A, B, C in a straight line through the foot of the tower are α, 2α, 3α, respectively. If AB = a, the height of the tower is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, OP be a vertical tower. The elevation of top P from A, B, C are α, 2α, 3α, respectively. ∠APB = 2α - α= ∠PAB.
Given :- AB = a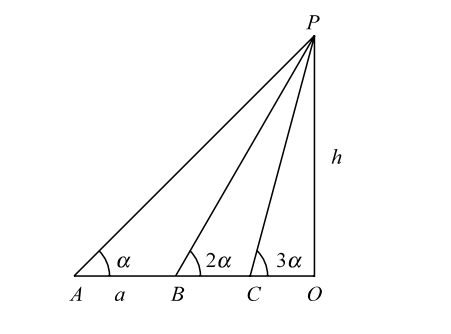
Correct Option: C
Let us draw the figure from the given question.
Let, OP be a vertical tower. The elevation of top P from A, B, C are α, 2α, 3α, respectively. ∠APB = 2α - α= ∠PAB.
Given :- AB = a
In triangle OBP ,∴ OP = sin 2α BP ∴ OP = BP sin 2α = a sin 2α. Thus, height of the tower = a sin 2α. 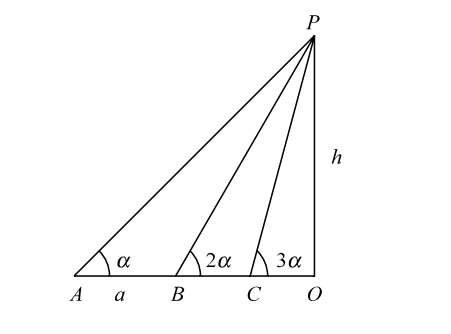
- A man is watching from the top of a tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man’s eye when at a distance of 60 meter from the tower. After 5 second, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming it is running in still water?
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Given :- time = 5 secondsIn triangle ACB , tan 45° = AB ⇒ AB = 60 m ....... ( 1 ) 60 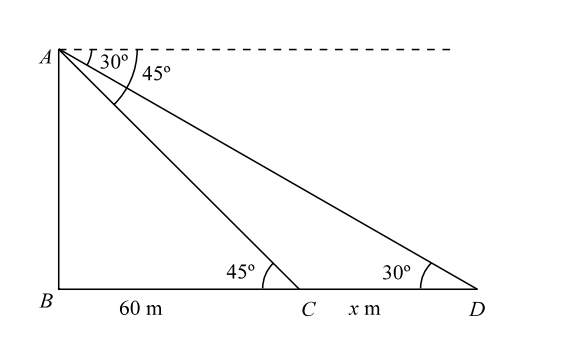
Correct Option: A
Let us draw the figure from the given question.
Given :- time = 5 secondsIn triangle ACB , tan 45° = AB ⇒ AB = 60 m ....... ( 1 ) 60 In triangle ADB , tan30° = AB , or, AB = 1 ( 60 + x ) ....... ( 2 ) 60 + x √3 From Equation (1) and Equation (2), 60 + x = 60 √3 ⇒ x = 60 ( √3 - 1 ) = 43.92 m ( Putting √3 = 1.732 ) ∴ Speed of the boat = Distance ( CD ) Time Speed of the boat = 43.92 m/s = 43.92 x 18 = 32 Km/h. 5 5 5 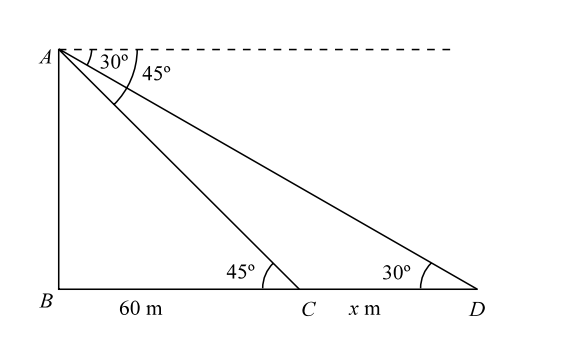
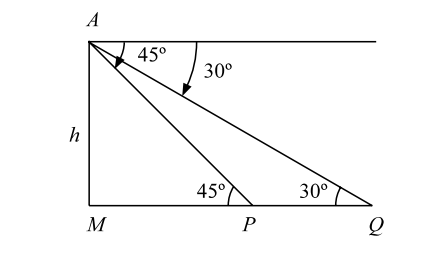
- Angle of depression from the top of a lighthouse of two boats are 45° and 30° due east which are 60 m apart. The height of the light house is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, the boats be at P, Q. So that PQ = 60m. Let, MA be the lighthouse.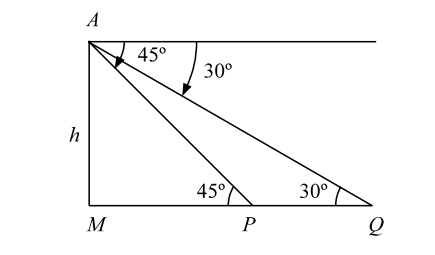
Correct Option: C
As per given figure , we have
Let, the boats be at P, Q. So that PQ = 60m. Let, MA be the lighthouse.
Let, h = MA.Then, h = tan45° = 1. ∴ h = MP MP Again, h = tan30° = 1 MP + 60 √3 ∴ MP + 60 = √3h or, h + 60 = √3h ∴ ( √3 - 1 )h = 60 ∴ h = 60 h = 60 ( √3 + 1 ) 30 ( √3 + 1 ) m √3 - 1 2