Height and Distance
- A 6 ft-tall man finds that the angle of elevation of the top of a 24 ft-high pillar and the angle of depression its base are complementary angles. Then the distance between pillar and man is ?
-
View Hint View Answer Discuss in Forum
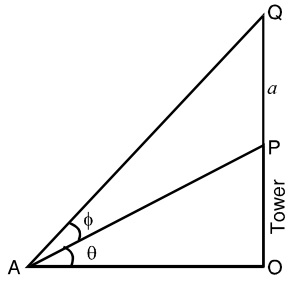
Let us draw a figure below from the given question.
Let AB = 24 ft and CD = 6 ft be the height of the pillar and man respectively.
Here ∠ ACE = ∝ ∠ CBD = 90° - ∝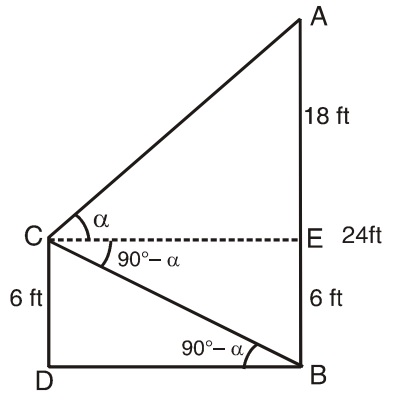
Correct Option: C
Let us draw a figure below from the given question.
Let AB = 24 ft and CD = 6 ft be the height of the pillar and man respectively.
Here ∠ ACE = ∝ ∠ CBD = 90° - ∝
Now from right triangle CDB,
BD = 6 cot (90° - ∝) = 6 tan ∝
∴ tan ∝ = BD/6 ...............(i)
From right triangle ACE,
tan ∝ =18/EC = 18/BD ...............(ii) (∵ EC = BD)
Now from (i) and (ii) we get,
BD/6 = 18/BD
⇒ BD2 = 18 x 6
∴ BD = 6√3 ft.
Hence, distance between pillar and man = 6√3 ft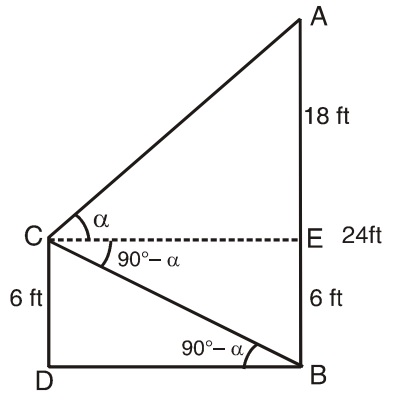
- At a point on a level plane a tower subtends an angle Θ and a flag-staff a ft. in length at the top of the tower subtends an angle Θ . The height of the tower is :
-
View Hint View Answer Discuss in Forum
Let us draw a figure below as per given question.
Let OP be the tower of height h (say) and PQ the flag-staff of height a, such that ∠OAP = Θ and ∠PAQ = Φ
In ΔOAP and ΔOAQ, Apply the formula
TanΘ = P/B = Perpendicular distance / Base distance
Proceed further and solve the given question by applying the above formula.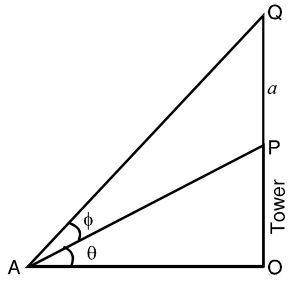
Correct Option: B
Let us draw a figure as per given question.
Let OP be the tower of height h (say) and PQ the flag-staff of height a, such that ∠OAP = Θ and ∠PAQ = Φ
In ΔOAP use the formula
TanΘ = P/B = Perpendicular distance / Base distance
⇒ TanΘ = OP/OA
⇒ OA = OP CotΘ
Put the value of OP in above equation, we will get
⇒ OA = hCotΘ ................ (1)
Now from triangle ΔOAQ,
⇒ Tan(Θ + Φ) = OQ/OA
⇒ OA = OQ Cot(Θ + Φ)
⇒ OA = (h + a) Cot(Θ + Φ) .............(2)
from equation (1) and (2), We will get
∴ hCotΘ = (h + a) Cot(Θ + Φ)
⇒ CotΘ / Cot(Θ + Φ) = (h + a) / h
⇒ CotΘ / Cot(Θ + Φ) = h / h + a / h
⇒ CotΘ / Cot(Θ + Φ) = 1 + a / h
⇒ (CotΘ / Cot(Θ + Φ)) - 1 = a / h
⇒ (CotΘ - Cot(Θ + Φ) ) / Cot(Θ + Φ) = a / h
⇒ h = aCot (Θ + Φ) / CotΘ - Cot(Θ + Φ)
After converting Cot into Sin and Cos, We will get
⇒ h = aSinΘCos(Θ + Φ)/SinΦ