-
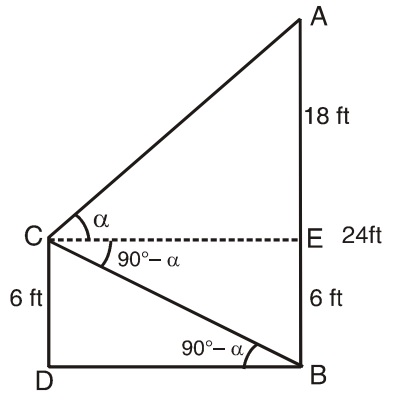
A 6 ft-tall man finds that the angle of elevation of the top of a 24 ft-high pillar and the angle of depression its base are complementary angles. Then the distance between pillar and man is ?
-
- 2√3 ft
- 4√3 ft
- 6√3 ft
- 8√3 ft
Correct Option: C
Let us draw a figure below from the given question.
Let AB = 24 ft and CD = 6 ft be the height of the pillar and man respectively.
Here ∠ ACE = ∝ ∠ CBD = 90° - ∝
Now from right triangle CDB,
BD = 6 cot (90° - ∝) = 6 tan ∝
∴ tan ∝ = BD/6 ...............(i)
From right triangle ACE,
tan ∝ =18/EC = 18/BD ...............(ii) (∵ EC = BD)
Now from (i) and (ii) we get,
BD/6 = 18/BD
⇒ BD2 = 18 x 6
∴ BD = 6√3 ft.
Hence, distance between pillar and man = 6√3 ft