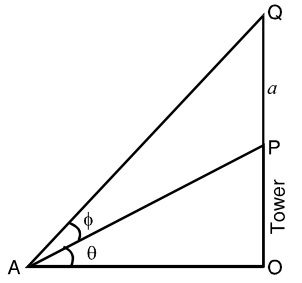
-
At a point on a level plane a tower subtends an angle Θ and a flag-staff a ft. in length at the top of the tower subtends an angle Θ . The height of the tower is :
-
- aSinΘCosΦ/Cos(Θ + Φ)
- aSinΘCos(Θ + Φ)/SinΦ
- aCos(Θ + Φ)/SinΘSinΦ
- None of these
Correct Option: B
Let us draw a figure as per given question.
Let OP be the tower of height h (say) and PQ the flag-staff of height a, such that ∠OAP = Θ and ∠PAQ = Φ
In ΔOAP use the formula
TanΘ = P/B = Perpendicular distance / Base distance
⇒ TanΘ = OP/OA
⇒ OA = OP CotΘ
Put the value of OP in above equation, we will get
⇒ OA = hCotΘ ................ (1)
Now from triangle ΔOAQ,
⇒ Tan(Θ + Φ) = OQ/OA
⇒ OA = OQ Cot(Θ + Φ)
⇒ OA = (h + a) Cot(Θ + Φ) .............(2)
from equation (1) and (2), We will get
∴ hCotΘ = (h + a) Cot(Θ + Φ)
⇒ CotΘ / Cot(Θ + Φ) = (h + a) / h
⇒ CotΘ / Cot(Θ + Φ) = h / h + a / h
⇒ CotΘ / Cot(Θ + Φ) = 1 + a / h
⇒ (CotΘ / Cot(Θ + Φ)) - 1 = a / h
⇒ (CotΘ - Cot(Θ + Φ) ) / Cot(Θ + Φ) = a / h
⇒ h = aCot (Θ + Φ) / CotΘ - Cot(Θ + Φ)
After converting Cot into Sin and Cos, We will get
⇒ h = aSinΘCos(Θ + Φ)/SinΦ