Height and Distance
- The angle of elevation of the top of a hill from each of the vertices A, B, C of a horizontal triangle is α. The height of the hill is :
-
View Hint View Answer Discuss in Forum
As per the given details of above question , we have
The distance of the foot from each vertex = h cotα.
∴ The foot is at the circumcentre of the triangle.
∴ R = h cotαCorrect Option: B
As per the given details of above question , we have
The distance of the foot from each vertex = h cotα.
∴ The foot is at the circumcentre of the triangle.
∴ R = h cotα∴ R = h tanα = a tanα = a tanα . cosecα . 2sinα 2
- The angle of elevation of the top of an unfinished tower at a point distant 120 m from its base is 45°. If the elevation of the top at the same point is to be 60°, the tower must be raised to a height :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Given :- OB = h + xh + x = tan 60° = √3 120 h + x = √3 (120) . 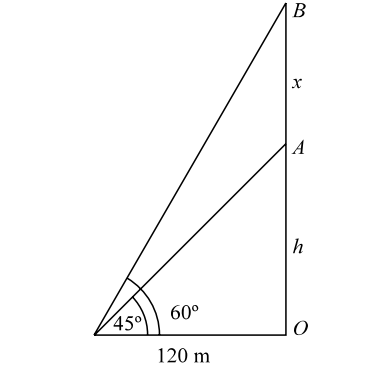
Correct Option: B
Let us draw the figure from the given question.
Given :- OB = h + x
In figure , we haveh + x = tan 60° = √3 120 h + x = √3 (120) ...........( 1 ) Also, h = tan 45° = 1 . 120 ∴ h = 120 m
From eq. ( 1 ) ,
∴ h + x = 120 + x = 120 √3∴ x = 120 ( √3 - 1 ) m . 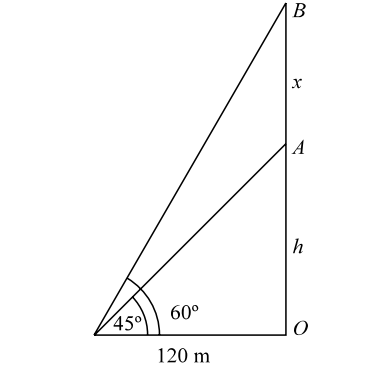
- A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60°. When he retires 40 m from the bank, he finds the angle to be 30°. The breadth of the river is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, OA denote the breadth of the river.
Given :- AB = 40 m
Correct Option: C
Let us draw the figure from the given question.
Let, OA denote the breadth of the river.
Given :- AB = 40 m
In triangle OAP , we haveOP = tan60° = √3 OA ∴ OP = √3 OA. Also, In triangle OBP , we have OP = tan 30° = 1 OA + 40 √3 ∴ OA + 40 = √3 OP = √3 ( √3 OA ) = 3 OA. ⇒ 2OA = 40 ⇒ OA = 20 m.
Hence , the breadth of the river = 20 m .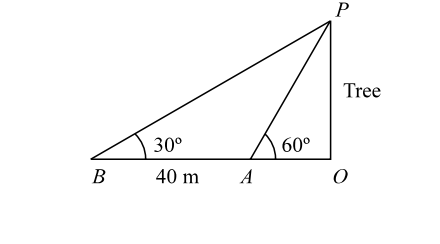
- The angle of elevation of the top of a tower at a point G on the ground is 30°. On walking 20 m towards the tower, the angle of elevation becomes 60°. The height of the tower is equal to :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, AB = h be the height of the tower. Let, GA = x.
Correct Option: D
Let us draw the figure from the given question.
Let, AB = h be the height of the tower. Let, GA = x and GH = 20 m.
In triangle BGA ,Then, h = tan30° = 1 . x √3 ∴ h = x ......... ( 1 ) √3 In triangle BHA , Also, h = tan60° = √3 . x - 20 ∴ h = √3 ( x - 20 ) ∴ x = √3 ( x - 20 ) [ using ( 1 ) ] √3 ⇒ x = 3 ( x - 20 ) = 3x - 60
Putting the value of x in eq. ( 1 ) , we get⇒ 2x = 60 ⇒ x = 30 . ∴ h = 30 = 10 √3 m . √3 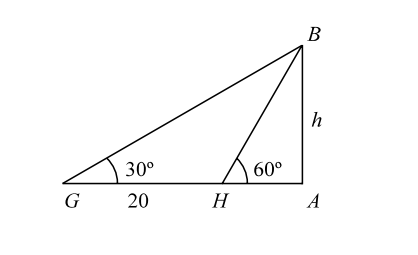
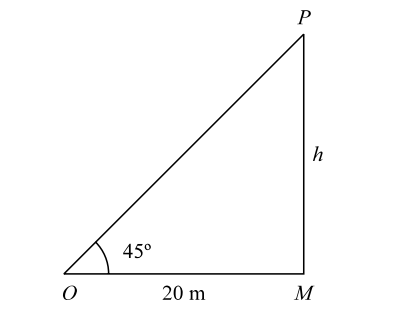
- The angle of elevation of the top of a tower from a point 20 m away from its base is 45°. The height of the tower is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let us assume the angle of elevation ∠MŌP = 45°.
Given :- MO = 20 m
In triangle MOP ,tan45° = PM MO Clearly, h = tan45 = 1 20 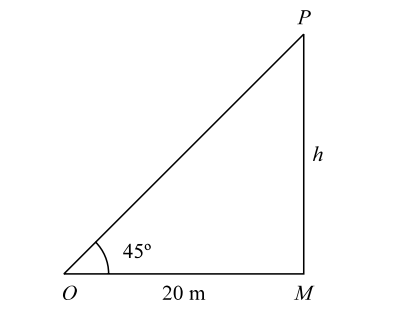
Correct Option: B
From the given figure , we can see that
Let us assume the angle of elevation ∠MŌP = 45°. and The height of the tower = h
Given :- MO = 20 m
In triangle MOP ,tan45° = PM MO ⇒ h = tan45° = 1 20
∴ h = 20 m