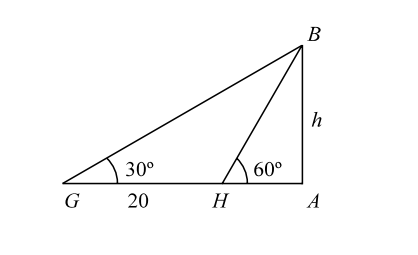
-
The angle of elevation of the top of a tower at a point G on the ground is 30°. On walking 20 m towards the tower, the angle of elevation becomes 60°. The height of the tower is equal to :
-
-
10 m √3 -
20 √3 m -
20 m √3 -
10 √3 m
-
Correct Option: D
Let us draw the figure from the given question.
Let, AB = h be the height of the tower. Let, GA = x and GH = 20 m.
In triangle BGA ,
| Then, | h | = | tan30° | = | 1 | . |
| x | √3 |
| ∴ | h = | x | ......... ( 1 ) | √3 |
| In triangle BHA , Also, | = | tan60° = | √3 . | x - 20 |
| ∴ | h = | √3 ( x - 20 ) |
| ∴ | x | = √3 ( x - 20 ) [ using ( 1 ) ] | √3 |
| ⇒ | x = | 3 ( x - 20 ) | = 3x - 60 |
| ⇒ | 2x = 60 | ⇒ | x = 30 . |
| ∴ | h = | 30 | = 10 √3 m . | √3 |