Height and Distance
- The angle of elevation of the top of an unfinished tower at a point distant 120 m from its base is 45°. If the elevation of the top at the same point is to be 60°, the tower must be raised to a height :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Given :- OB = h + xh + x = tan 60° = √3 120 h + x = √3 (120) . 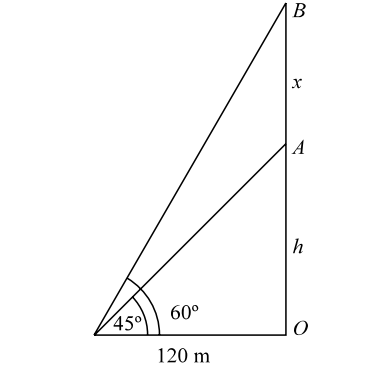
Correct Option: B
Let us draw the figure from the given question.
Given :- OB = h + x
In figure , we haveh + x = tan 60° = √3 120 h + x = √3 (120) ...........( 1 ) Also, h = tan 45° = 1 . 120 ∴ h = 120 m
From eq. ( 1 ) ,
∴ h + x = 120 + x = 120 √3∴ x = 120 ( √3 - 1 ) m . 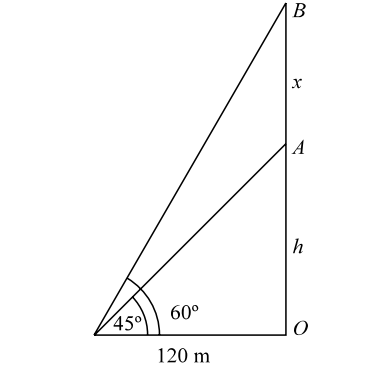
- A man from the top of a 100 m high tower sees a car moving towards the tower at an angle of depression of 30°. After some time, the angle of depression becomes 60°. The distance (in m) traveled by the car during this time is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
C = Initial point and
D = Final point
AB = Tower = 100 m
Let CD be x m.
From ΔABD,
Correct Option: B
Let us draw the figure from the given question.
C = Initial point and
D = Final point
AB = Tower = 100 m
Let CD be x m.
From ΔABD,tan 60° = AB BD ⇒ √3 = 100 BD ⇒ BD = 100 m √3 From ΔABC, tan 30° = AB BC ⇒ 1 = 100 √3 100 + x √3 ⇒ 100 + x = 100 √3 √3 ∴ x = 100 √3 - 100 √3 x = 300 - 100 = 200 = 200 √3 m √3 √3 3 The distance (in m) travelled by the car during this time is 200 √3 m 3
- The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is
-
View Hint View Answer Discuss in Forum
Let AB be the wall and BC be the ladder.
Then, ∠ ACB = 60° and AC = 4.6 m.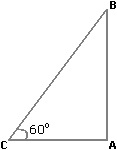
Correct Option: D
Let AB be the wall and BC be the ladder.
Then, ∠ ACB = 60° and AC = 4.6 m.
AC/BC = cos 60° = 1/2
BC = 2 x AC
= (2 x 4.6) m
= 9.2 m.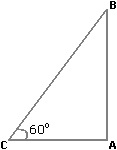
-
sin A + sin A is ( 0° < A < 90° ) . 1 + cos A 1 - cos A
-
View Hint View Answer Discuss in Forum
As per given question , we have
sin A + sin A 1 + cos A 1 - cos A
Correct Option: A
As per given question , we have
sin A + sin A 1 + cos A 1 - cos A sin A + sin A = sin A( 1 - cos A ) + sin A( 1 + cos A ) 1 + cos A 1 - cos A ( 1 + cos A )( 1 - cos A ) = sin A - sin A cos A + sin A sin A cos A 1 + cos2 A = 2 sin A = 2 cosec A sin2 A ∴ sin A + sin A = 2cosec A 1 + cos A 1 - cos A
- The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes P meter smaller. The value of P is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, AB be the tower and AC and AD be its shadows.
Then, AB = 100 m.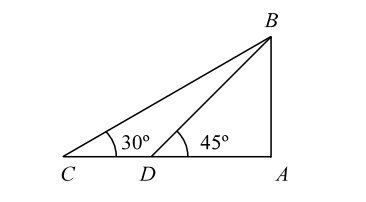
Correct Option: C
As per given figure , we have
Let, AB be the tower and AC and AD be its shadows.
Then, AB = 100 m.
In triangle BDA ,AD = cot45° = 1 ⇒ AD = 1 AB 100
⇒ AD = 100 m.
And In triangle BCA ,AC = cot30° = √3 ⇒ AC = √3 AB 100
⇒ AC = 100 √3 m.
∴ P = AC - AD = 100(√3 - 1) m.
Hence ,The value of P is 100(√3 - 1) m.