Height and Distance
- From a point P on a level ground, the angle of elevation of the top of a tower is 30°, if the tower is 100 m high, find the distance of point P from the foot of the tower.
-
View Hint View Answer Discuss in Forum
Let us draw a figure from given question.
Let, AB = 100 m be the height of a tower, P is a point on the ground such that ∠APB = 30°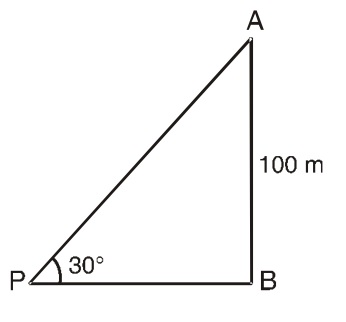
Correct Option: B
Let us draw a figure from given question.
Let, AB = 100 m be the height of a tower, P is a point on the ground such that ∠APB = 30°
From right triangle ABP,
BP = 100 cot 30°
⇒ BP = 100 √3
⇒ BP = 100 X 1.73
⇒ BP = 173 meter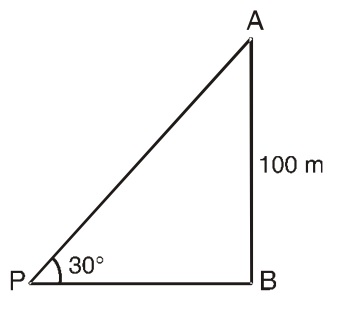
- A man is observing from the top of a tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man's eye when at a distance of 60 m from the tower. After 5 second, the angle of depression becomes 30°, Find the speed of the boat, assuming that it is running in still water.
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let AB = h meter be the height of the tower; C and D are the two points on the ground such that BC = 60 m; ∠ACB = 45° and ∠ADB = 30°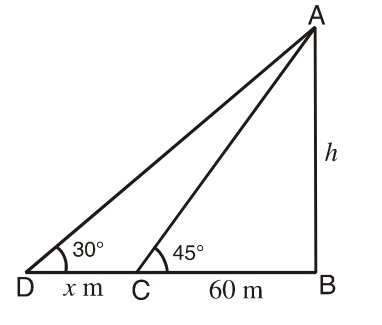
Correct Option: B
Let us draw the figure from the given question.
Let AB = h meter be the height of the tower; C and D are the two points on the ground such that BC = 60 m; ∠ACB = 45° and ∠ADB = 30°
Now from right triangle ABC,
tan 45° = h/60
⇒ 1 = h/60
∴ h = 60 m;
Again from right triangle ABD;
tan 30° = h/(x + 60)
⇒ 1/√3 = 60/(x + 60)
⇒ x + 60 = 60√3
∴ x = 60(1.73 - 1) = 43.8 meter
Hence, speed of boat = 43.8/5 m/s = 43.8/5 x 18/5 = 31.5 km/hr.
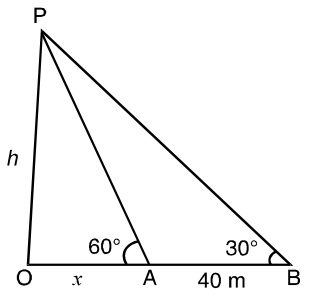
- A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60°, when he retires 40 meters from the bank then he find the angle to be 30°. Then the breadth of the river is ?
-
View Hint View Answer Discuss in Forum
Let us draw a figure below as per given question.
Let A be the position of a person on the bank of a river and OP the tree on the opposite bank and ∠OAP = 60°. When the person retires to the position B, then AB = 40 meter and ∠OBP = 30°
Use the trigonometry formula to solve the given question.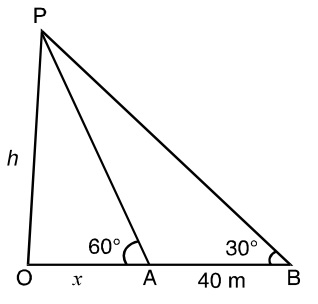
Correct Option: C
Let us draw a figure below as per given question.
Let A be the position of a person on the bank of a river and OP the tree on the opposite bank and ∠OAP = 60°. When the person retires to the position B, then AB = 40 meter and ∠OBP = 30°
Let us assume OA(Breadth of the river) = x meter and height of tree OP = h meter
In ΔOAP, Use the trigonometry formula
Tan60° = P/B = Perpendicular distance / Base distance
⇒ Tan60° = OP / OA
⇒ OP = OA Tan60°
Put the value of OP and OA, We will get
⇒ h = x√3 ..............(1)
Now in the triangle ΔOBP
Tan30° = OP / OB
⇒ OP = OB Tan30°
⇒ OP = (x + 40)/√3
⇒ h = (x + 40)/√3 ...................(2)
From Equation (1) and (2), We will get
⇒ (x + 40)/√3 = x√3
⇒ (x + 40) = x√3 X √3
⇒ (x + 40) = 3x
⇒ 3x - x = 40
∴ x = 20 m