Height and Distance
- The angle of elevation of the top of a tower from a point 20 m away from its base is 45°. The height of the tower is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let us assume the angle of elevation ∠MŌP = 45°.
Given :- MO = 20 m
In triangle MOP ,tan45° = PM MO Clearly, h = tan45 = 1 20 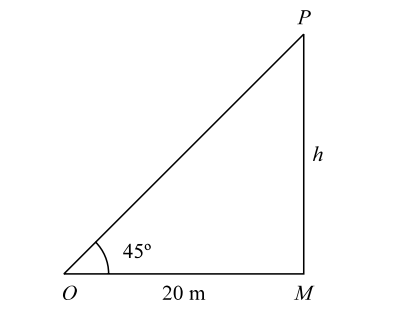
Correct Option: B
From the given figure , we can see that
Let us assume the angle of elevation ∠MŌP = 45°. and The height of the tower = h
Given :- MO = 20 m
In triangle MOP ,tan45° = PM MO ⇒ h = tan45° = 1 20
∴ h = 20 m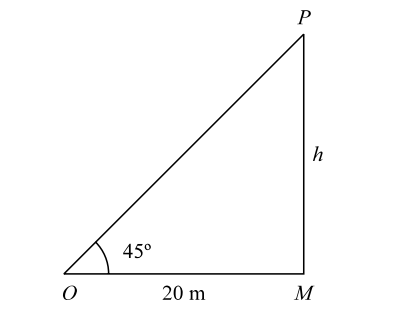
- From the top of a 25 m high, cliff the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. Find out the height of the tower.
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, AB be the cliff and CD be the tower. From B, draw BE ⊥ CD.
Let us assume the angle of elevation ∠ACB = ∠EBD = α.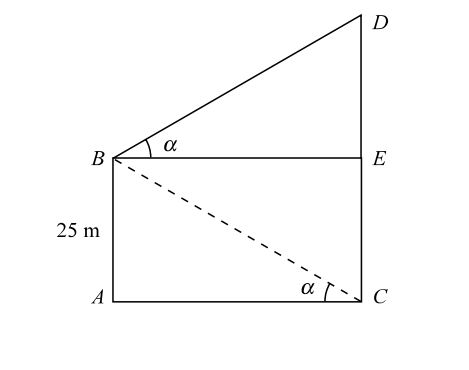
Correct Option: C
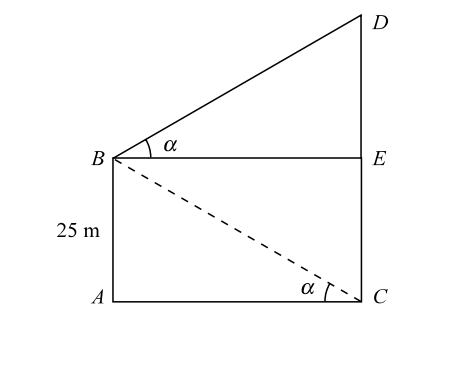
From the figure , we can see that
Let, AB be the cliff and CD be the tower. From B, draw BE ⊥ CD.
Given :- AB = 25 m
In triangle EBD and ACB , we haveDE = tan α and AB = tan α BE AC ⇒ DE = AB BE AC
∴ DE = AB ( ∵ BE = AC)
∴ CD = CE + DE = AB + AB = 2AB = 2 x 25 = 50 m.
- The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 12.4 m away from the wall. The length of the ladder is :
-
View Hint View Answer Discuss in Forum
Consider the diagram is shown above where PR represents the ladder and RQ represent the wall.
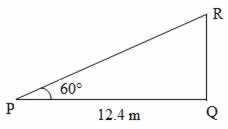
Correct Option: B
Consider the diagram is shown above where PR represents the ladder and RQ represent the wall.
Cos 60° = PQ / PR
⇒ 1 / 2 = 12.4 / PR
⇒ PR = 2 × 12.4 = 24.8 m
- A tower stands at the end of a straight road. The angles of elevation of the top of the tower from two points on the road 500 m apart are 45° and 60°, respectively. Find out the height of the tower.
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Given , CD = 500 m , θ1 = 45° and θ2 = 60°
We know that(cot 45° - cot 60°) = CD AB
⇒ CD = AB (cot 45° - cot 60°)⇒ AB = CD (cot 45° - cot 60°) 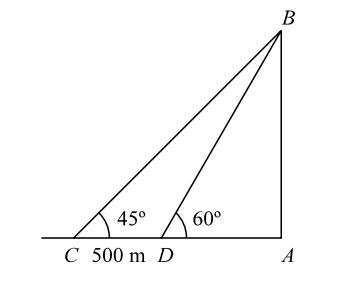
Correct Option: A
From given figure , we can see that
Given , CD = 500 m , θ1 = 45° and θ2 = 60°
We know that(cot 45° - cot 60°) = CD AB
⇒ CD = AB (cot 45° - cot 60°)⇒ AB = CD (cot 45° - cot 60°) ⇒ AB = 500 = 500 √3 m. 1 - 1 √3 - 1 √3 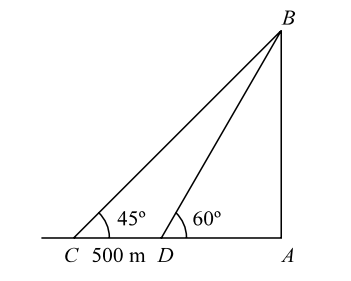
- When the sun is 30° above the horizontal, the length of shadow cast by a building 50 m high is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, AB be the building and AC be its shadow.
Then, height of building AB = 50 m and θ = 30°.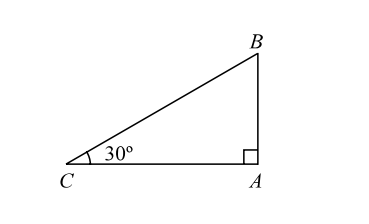
Correct Option: B
Let us draw the figure from the given question.
Let, AB be the building and AC be its shadow.
Then, height of building AB = 50 m and θ = 30°.In triangle ACB , cotθ = AC AB ∴ AC = cot 30° = √3 ⇒ AC = √3 AB 50
⇒ AC = 50 √3 m.
Hence , the length of shadow cast by a building 50 m high is 50 √3 m .

