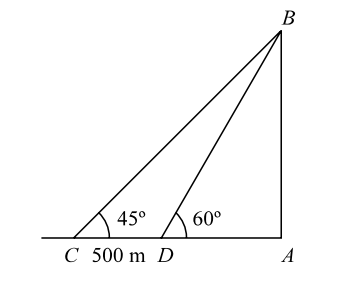
-
A tower stands at the end of a straight road. The angles of elevation of the top of the tower from two points on the road 500 m apart are 45° and 60°, respectively. Find out the height of the tower.
-
-
500 √3 √3 - 1 - 5000 √3
-
500 √3 √3 + 1 - None of these
-
Correct Option: A
From given figure , we can see that
Given , CD = 500 m , θ1 = 45° and θ2 = 60°
We know that
| (cot 45° - cot 60°) = | CD |
| AB |
⇒ CD = AB (cot 45° - cot 60°)
| ⇒ AB | = | |
| (cot 45° - cot 60°) |
| ⇒ AB = | 500 | = | 500 √3 | m. | |
| 1 - | 1 | √3 - 1 | |||
| √3 | |||||