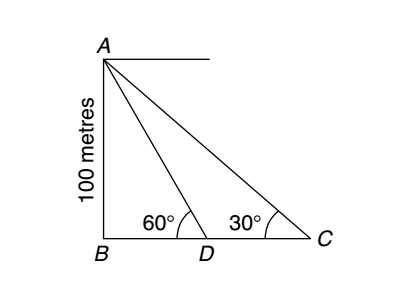
-
A man from the top of a 100 m high tower sees a car moving towards the tower at an angle of depression of 30°. After some time, the angle of depression becomes 60°. The distance (in m) traveled by the car during this time is :
-
- 100 √3
-
200 √3 3 -
100 √3 3 - 200 √3
Correct Option: B
Let us draw the figure from the given question.
C = Initial point and
D = Final point
AB = Tower = 100 m
Let CD be x m.
From ΔABD,
| tan 60° | = | AB | BD |
| ⇒ | √3 | = | 100 | BD |
| ⇒ | BD | = | 100 | m | √3 |
| From ΔABC, |
| tan 30° | = | AB | BC |
| ⇒ | = | |||
| √3 | 100 | + x | ||
| √3 | ||||
| ⇒ | 100 | + x = | 100 √3 |
| √3 |
| ∴ | x = | 100 √3 - | 100 |
| √3 |
| x = | 300 - 100 | = | 200 | = | 200 √3 | m |
| √3 |
| The distance (in m) travelled by the car during this time is | 200 √3 | m |