-
A tower standing on a horizontal plane subtends a certain angle at a point 160 m apart from the foot of the tower. On advancing 100 m towards it, the tower is found to subtend an angle twice as before. The height of the tower is :
-
- 80 m
- 100 m
- 160 m
- 200 m
Correct Option: A
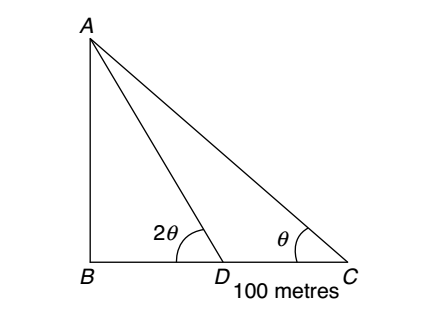
Let us draw the figure from the given question.
Let Tower AB = h m
Given :- CD = 100 m ; BC = 160 m , BD = 160 - 100 = 60 m
∠ACB = θ ∴ ∠ADB = 2θ
In ΔABC,
| tanθ | = | AB | ⇒ | tanθ = | |
| BC | 160 |
| In ΔABC, |
| tan 2θ | = | AB | = | |
| BD | 60 |
| ⇒ | = | ||
| 1 - tan2 θ | 60 |
| ⇒ | 2 x | = | |
| h | |||
| 1 - | 60 | ||
| 160 × 160 |
| ⇒ | = | ||||
| 80 ( 1 - | ) | 60 | |||
| 160 × 160 | |||||
| ⇒ | 4 ( 1 - | ) | = 3 | |
| 160 × 160 |
| ⇒ | = 1 - | 3 | = | 1 | ⇔ | h2 = 6400 | |
| 160 × 160 | 4 | 4 |
| h = √6400 = 80 m |
Hence ,the height of the tower is 80 m .