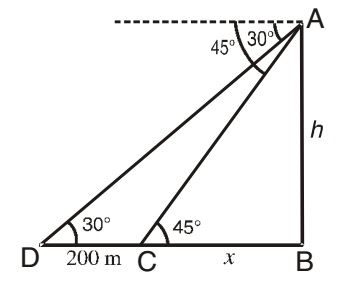
-
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. if the ships are 200 m apart, find the height of the light house .
-
- 100 m
- 173 m
- 200 m
- 273 m
Correct Option: D
Let us draw a figure below as per given question.
Let AB = h meter be the height of the tower and two ships are situated at D and C respectively; such that, CD = 200 m; ∠ADC = 30° ∠ACB = 45° and BC = x meter (say)
Now from right triangle ABC,
tan 45° = h/x ⇒ 1 = h/x
∴ x = h
Again from right triangle ABD,
tan 30° = h/( 200 + x )
⇒ 1/√3 = h/( 200 + x )
Since x = h , we will get.
⇒ 1/√3 = h/(200 + h )
⇒ (200 + h ) = h X √3
⇒ h X √3 - h = 200
⇒ h x 1.732 - h = 200
⇒ h(1.732 - 1) = 200
∴ h = 200/0.732 = 273.2 m = 273 m