Height and Distance
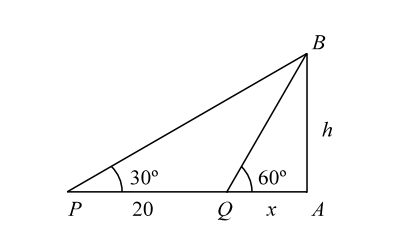
- On the level ground, the angle of elevation of the top of the tower is 30°. On moving 20 m nearer, the angle of elevation is 60°. The height of the tower is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, h be the height of the tower.
Let us assume the angle of elevation ∠APB = 30° and ∠AQB = 60°.
In triangle AQB ,h = tan60° = √3. x 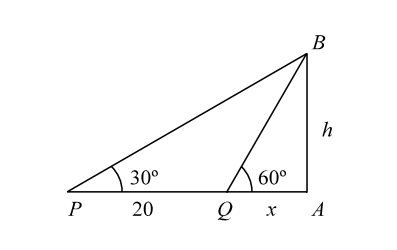
Correct Option: B
Let, h be the height of the tower.
Let us assume the angle of elevation ∠APB = 30° and ∠AQB = 60°.
In triangle AQB and APB , we havetan60° = AB AQ ⇒ h = tan60° = √3. x
∴ h = √3x .......... ( 1 )And tan30° = AB AP ⇒ h = tan30° = 1 20 + x √3
⇒ √3 h = 20 + x
⇒ √3 (√3x) = 20 x [ From equation ( 1 ) ]
⇒ 3x = 20 + x
∴ x = 10.
Putting the value of x in equation ( 1 ) , we get
∴ h = 10 √3 m.
- The angles of depression of two ships from the top of a light house are 45° and 30° towards east. if the ships are 200 m apart, find the height of the light house .
-
View Hint View Answer Discuss in Forum
Let us draw a figure below as per given question.
Let AB = h meter be the height of the tower and two ships are situated at D and C respectively; such that, CD = 200 m; ∠ADC = 30° ∠ACB = 45° and BC = x meter (say)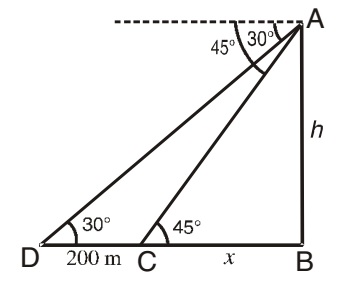
Correct Option: D
Let us draw a figure below as per given question.
Let AB = h meter be the height of the tower and two ships are situated at D and C respectively; such that, CD = 200 m; ∠ADC = 30° ∠ACB = 45° and BC = x meter (say)
Now from right triangle ABC,
tan 45° = h/x ⇒ 1 = h/x
∴ x = h
Again from right triangle ABD,
tan 30° = h/( 200 + x )
⇒ 1/√3 = h/( 200 + x )
Since x = h , we will get.
⇒ 1/√3 = h/(200 + h )
⇒ (200 + h ) = h X √3
⇒ h X √3 - h = 200
⇒ h x 1.732 - h = 200
⇒ h(1.732 - 1) = 200
∴ h = 200/0.732 = 273.2 m = 273 m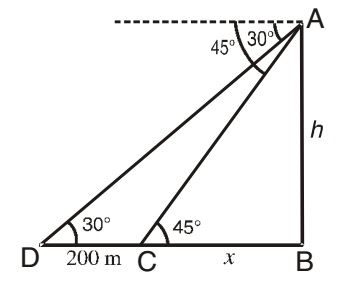
- In a rectangle, if the angle between a diagonal and a side is 30° and the length of diagonal is 6 cm, the area of the rectangle is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, ABCD be the rectangle in which ∠BAC = 30° and AC = 6 cm.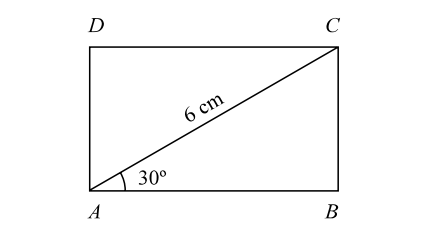
Correct Option: B
As per given figure , we can see that
Let, ABCD be the rectangle in which ∠BAC = 30° and AC = 6 cm.
In triangle BAC , we haveAB = cos30° = √3 ⇒ AB = 3 √3 cm. AC 2 BC = sin30° = 1 ⇒ BC = 3 cm. AC 2
∴ Area of the rectangle = Length x Breadth = AB X BC = 9 √3 cm2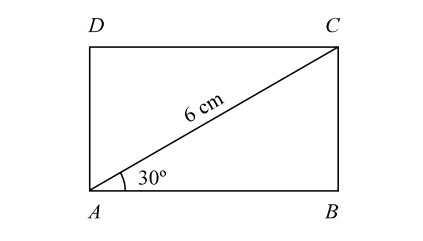
- The upper part of a tree broken by the wind makes an angle of 30° with the ground and the distance from the root to the point where the top of the tree touches the ground is 10 m. What was the height of the tree?
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, QMP be the tree. When broken by the wind, its top P strikes the ground at A such that ∠QAM = 30°, AQ = 10m and MA = MP.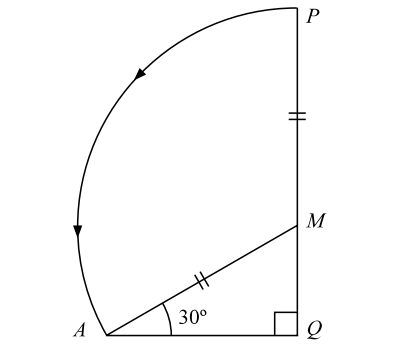
Correct Option: A
Let us draw the figure from the given question.
Let, QMP be the tree. When broken by the wind, its top P strikes the ground at A such that ∠QAM = 30°, AQ = 10m and MA = MP.
In figure QAM , we know thatMQ = tan30° ⇒ MQ = 10 m AQ √3 and, AM = sec30° ⇒ AM = 10 ( 2 ) = 20 AQ √3 √3 ∴ Height of the tree = QM + MP = QM + AM = 10 + 20 √3 √3 Height of the tree = 30 = 10 √3 [ Multiplying by √3 in numerator and denominator both ] √3
Hence , Height of the tree = 10 √3 m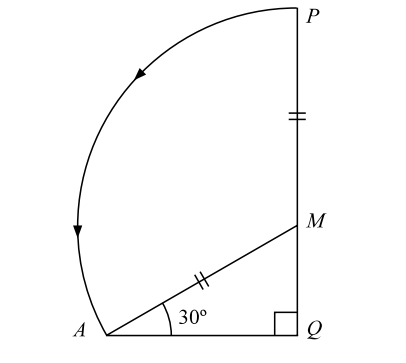
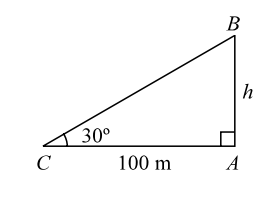
- A tower stands on a horizontal plane. A man on the ground 100 m from the base of the tower finds the angle of elevation of the top of the tower to be 30°. What is the height of the tower?
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Given :- θ = 30° , AB = h and AC = 100 mIn triangle ACB , tanθ = AB AC tan 30° = h 100 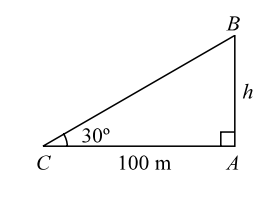
Correct Option: C
Let us draw the figure from the given question.
Given :- θ = 30° , AB = h and AC = 100 mIn triangle ACB , tanθ = AB AC tan 30° = h 100 ⇒ 1 = h √3 100 ⇒ h = 100 m. √3 Hence , the height of the tower is 100 √3