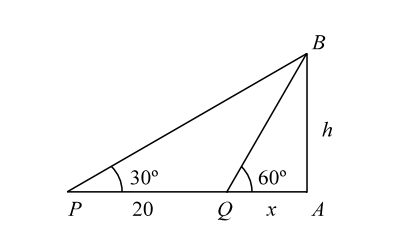
-
On the level ground, the angle of elevation of the top of the tower is 30°. On moving 20 m nearer, the angle of elevation is 60°. The height of the tower is :
-
- 20 √3 m
- 10 √3 m
- 10 ( √3 - 1 ) m
- None of these
Correct Option: B
Let, h be the height of the tower.
Let us assume the angle of elevation ∠APB = 30° and ∠AQB = 60°.
In triangle AQB and APB , we have
| tan60° = | AB | AQ |
| ⇒ | h | = | tan60° | = | √3. |
| x |
∴ h = √3x .......... ( 1 )
| And tan30° = | AB | AP |
| ⇒ | = | tan30° | = | 1 | |
| 20 + x | √3 |
⇒ √3 h = 20 + x
⇒ √3 (√3x) = 20 x [ From equation ( 1 ) ]
⇒ 3x = 20 + x
∴ x = 10.
Putting the value of x in equation ( 1 ) , we get
∴ h = 10 √3 m.