Height and Distance
- At a point on a level plane a tower subtends an angle θ and a flag-staff a ft. in length at the top of the tower subtends an angle ɸ. The height of the tower is :
-
View Hint View Answer Discuss in Forum
Let OP be the tower of height h (say) and PQ the flag-staff of height a, such that
∠OAP = θ and ∠PAQ = ɸ
In ΔOAP and ∠OAQCorrect Option: D
Let OP be the tower of height h (say) and PQ the flag-staff of height a, such that
∠OAP = θ and ∠PAQ = ɸ
In ΔOAP and ∠OAQ
OA = OP cot θ = h cotθ
and OA = OQ cot ( θ + ɸ ) = (h + a) cot ( θ + ɸ )
∴ h cotθ = (h + a) cot ( θ + ɸ )
⇒ h = a cot ( θ + ɸ ) / cotθ - cot ( θ + ɸ )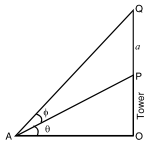
- The height of the center of the round balloon of radius r, which subtend an angle ∝ at the eye of an observer and the elevation of whose center from the eye is β, is given by ?
-
View Hint View Answer Discuss in Forum
Let O be the center of the balloon of radius r which subtend an angle ∝ at the eye of an observer at E.
If EA and EB are the tangents to the balloon,
then ∠ OEA = ∠ OEB = ∝/2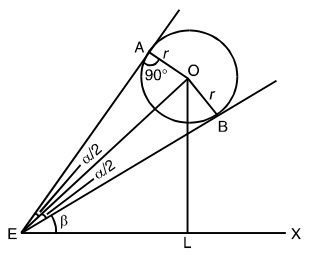
Correct Option: B
Let O be the centre of the balloon of radius r which subtend an angle ∝ at the eye of an observer at E .
If EA and EB are the tangents to the ballon,
then ∠ OEA = ∠ OEB = ∝/2
In triangle ΔOAE, Sin ∝/2 = OA/OE
∴ OE = r cosec 1/2 ∝
In ∠OEL, height of the center of the balloon = h = OE sin β = r Cosec ∝/2 Sin β.
- ABCD is a square plot. The angle of elevation of the top of a pole standing at D from A or C is 30° and that from B is Θ then Tan Θ equal to ?
-
View Hint View Answer Discuss in Forum
Let us draw a figure below from given question.
Let a be the length of a side of square plot ABCD and h, the height of the pole standing at D. Since elevations of P from A or C is 30° and that from B is Θ,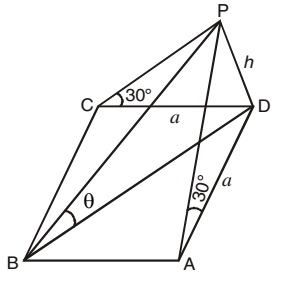
Correct Option: B
Let a be the length of a side of square plot ABCD and h, the height of the pole standing at D. Since elevations of P from A or C is 30° and that from B is Θ,
∴ In triangle Δ PCD, tan 30° = h/a
i.e h/a = 1/√3 .............. (1)
And in triangle Δ PBD,
Since PD = h and BD = √(AB2 + AD)2 = a√2.
Put the value of PD and BD , we will get
tan Θ = PD/BD = h/(a√2)
put the value of h/a from equation (1)
tan Θ = 1/√2 x 1/√3
tan Θ = 1/√6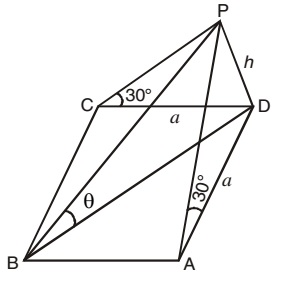
- ABC is a triangular park with AB = AC = 100 meters. A clock tower is situated at the mid-point of BC. The angles of elevation of the top of the tower of A and B are cot-1 (3.2) and cosec-1(2.6) respectively. The height of the tower in meters is ?
-
View Hint View Answer Discuss in Forum
Let us draw a figure as per given question.
Given ∝ = cot-1 (3.2) and β = cosec-1(2.6)
In triangle ΔPAD, AD = h cot ∝
In triangle ΔPBD, BD = h cot β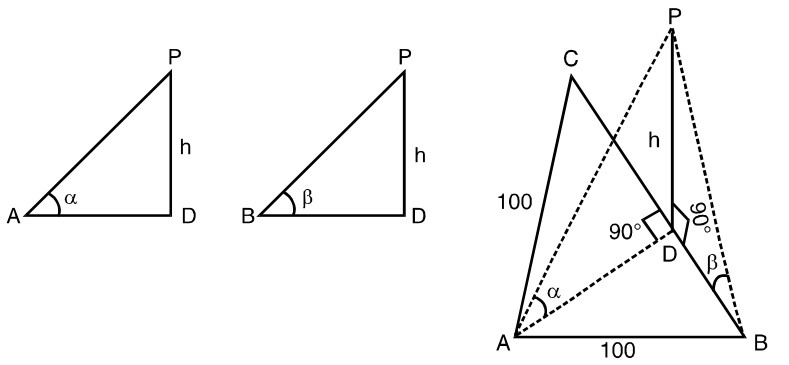
Correct Option: B
Let us draw a figure below as per given question.
Given ∝ = cot-1 (3.2) and β = cosec-1(2.6)
In triangle ΔPAD, AD = h cot ∝
In triangle ΔPBD, BD = h cot β
In triangle Δ ABD,
AB2 = AD2 + BD2
= h2(cot2∝ + cot2 β )
⇒ 1002 = h2{ cot2 ∝ + (cosec2 β - 1) }
⇒ 1002= h2 { (3.2)2 + (2.6)2 - 1} = 16h2
⇒ h = 25 m.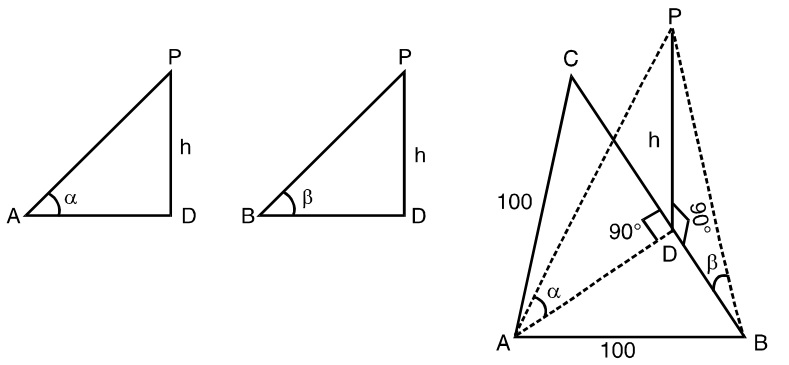
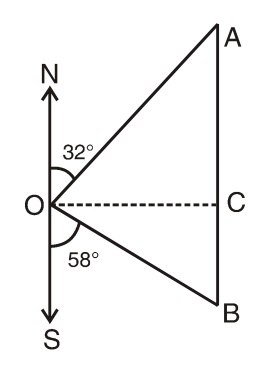
- Two ships leave a port at the same instant. One sails at 30km/hr in the direction N 32° E while the other sails at 20 km/hr in the direction S 58° E. After two hours the ships are distant from each other by.
-
View Hint View Answer Discuss in Forum
Let us draw a figure below as per given question.
Let two ships started from point O at the speed of 30 km/hr and 20 km/hr respectively, after two hours they reach at points A and B.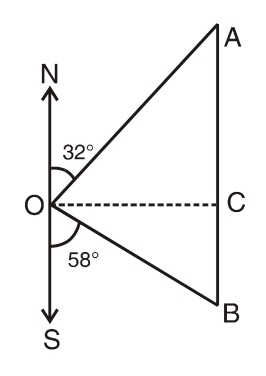
Correct Option: C
Let us draw a figure below as per given question.
Let two ships started from point O at the speed of 30 km/hr and 20 km/hr respectively, after two hours they reach at points A and B.
Now, ∠NOA = 32° and ∠SOB = 58° ,
Then, ∠AOB = 180° - (32° + 58°) = 90°
Since ΔAOB is a right triangle in which OA = 2 x 30 = 60 km and OB = 2 x 20 = 40 km
Since, AB = √OA2 + OB2
= √(60)2 + (40)2
= √5200
= 20√13