Height and Distance
- A man is standing on the 8 m long shadow of a 6 m long pole. If the length of the shadow is 2.4 meter, then the height of the man is :
-
View Hint View Answer Discuss in Forum
As per the details of given above question , we have
Let, h be the height of the man.
Given :- The length of the shadow = 2.4 m
The length of the shadow of the pole = 8 m and the height of the pole = 6 mCorrect Option: C
As per the details of given above question , we have
Let, h be the height of the man.
Given :- The length of the shadow of the man = 2.4 m
The length of the shadow of the pole = 8 m and the height of the pole = 6 m∴ height of the pole = height of the man shadow of the pole shadow of the man ⇒ 6 = h ⇒ h = 3 ( 2.4 ) = 1.8 m. 8 2.4 4
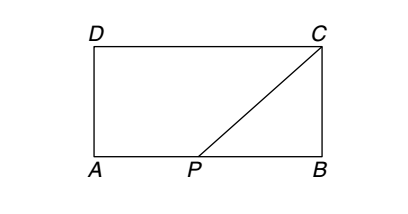
- ABCD is a rectangle where the ratio of the lengths of AB and BC is 3 : 2. If P is the midpoint of AB, then the value of sin (∠CPB) is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let Length AB = 3y units
Breadth BC = 2y units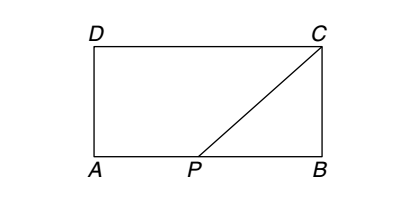
Correct Option: D
Let us draw the figure from the given question.
Let Length AB = 3y units
Breadth BC = 2y unitsPB = 3 y units 2 CP = √PB2 + BC2 = √( 9y2/4 ) + 4y2 CP = √ 25y2 4 CP = 5y units 2 sin∠CPB = BC = 2y = 4 CP 5y/2 5
-
The length of a shadow of a vertical tower is 1 √3 times of its height. The angle of elevation of the Sun is :
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
Let, AB be tower and BC be its shadow.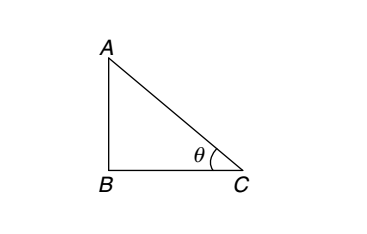
Correct Option: C
Let us draw the figure from the given question.
Let, AB be tower and BC be its shadow.Given :- AB = x, then BC = x √3 ∴ tan θ = AB = x = √3 BC x √3 ∴ tan θ = tan 60° ⇒ θ = 60° 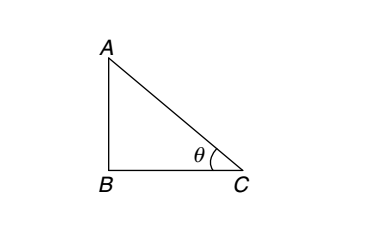
- The angles of elevation of the top of a tower from the points P and Q, at distances of ‘a’ and ‘b’ respectively from the base of the tower and in the same straight line with it are complementary. The height of the tower is :
-
View Hint View Answer Discuss in Forum
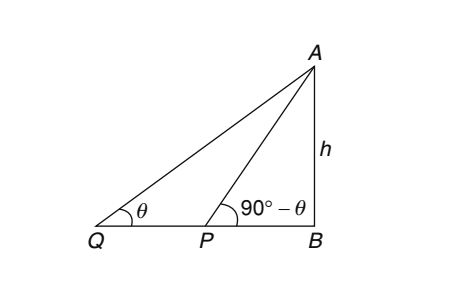
Let us draw the figure from the given question.
Let AB = Tower = h units
∴∠AQB = θ ∴ ∠ APB= 90° − θ
PB = a; BQ = b
From ΔAQB,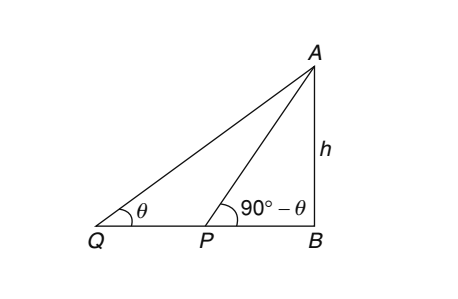
Correct Option: A
Let us draw the figure from the given question.
Let AB = Tower = h units
∴∠AQB = θ ∴ ∠ APB= 90° − θ
PB = a; BQ = b
From ΔAQB,tan θ = AB BQ ⇒ tan θ = h ..... ( 1 ) b From ΔAQB, tan( 90° - θ ) = h PB
By multiplying both the equations, we have⇒ cot θ = h ...... ( 2 ) a tan θ . cot θ = h × h b a ⇒ h2 = ab ⇔ h = √ab
Hence ,the height of the tower is √ab .
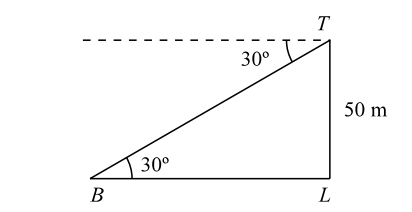
- From the top of a lighthouse, 50 m above the sea, the angle of depression of an incoming boat is 30°. How far is the boat from the lighthouse?
-
View Hint View Answer Discuss in Forum
Let us draw the figure from the given question.
TL = 50 m , θ = 30°
In triangle TBL ,tan30° = TL BL 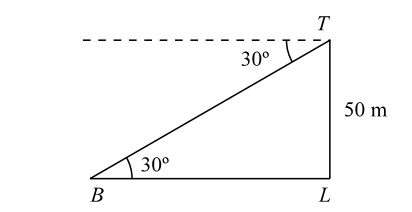
Correct Option: C
From given figure , we have
TL = 50 m , θ = 30°
In triangle TBL ,tan30° = TL ⇒ 1 = 50 BL √3 BL
∴ BL = 50 √3 m.
The boat from the lighthouse far is 50 √3 m.