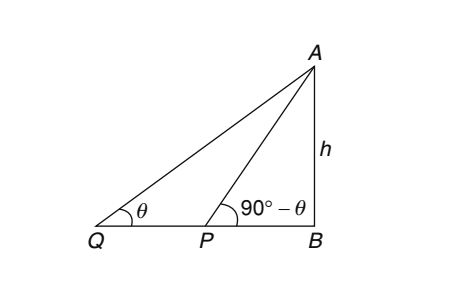
The angles of elevation of the top of a tower from the points

The angles of elevation of the top of a tower from the points P and Q, at distances of ‘a’ and ‘b’ respectively from the base of the tower and in the same straight line with it are complementary. The height of the tower is :

Let us draw the figure from the given question.
Let AB = Tower = h units
∴∠AQB = θ ∴ ∠ APB= 90° − θ
PB = a; BQ = b
From ΔAQB,

tan θ	=	AB
		BQ

⇒	tan θ	=	h	..... ( 1 )
			b

From ΔAQB,

tan( 90° - θ )	=	h
		PB

⇒	cot θ	=	h	...... ( 2 )
			a

By multiplying both the equations, we have

tan θ . cot θ	=	h	×	h
		b		a

⇒

h² = ab

⇔

h = √ab

Hence ,the height of the tower is √ab .