-
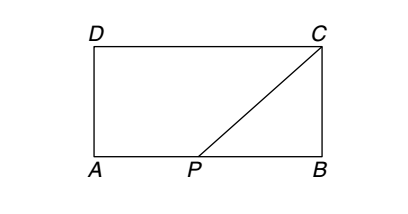
ABCD is a rectangle where the ratio of the lengths of AB and BC is 3 : 2. If P is the midpoint of AB, then the value of sin (∠CPB) is :
-
-
3 5 -
2 5 -
3 4 -
4 5
-
Correct Option: D
Let us draw the figure from the given question.
Let Length AB = 3y units
Breadth BC = 2y units
| PB | = | 3 | y units | 2 |
| CP | = | √PB2 + BC2 = √( 9y2/4 ) + 4y2 |
| CP = √ | 25y2 | |
| 4 |
| CP = | 5y | units |
| 2 |
| sin∠CPB = | BC | = | 2y | = | 4 |
| CP | 5y/2 | 5 |