-
From the top of a tower of height 108 meter the angles of depression of two objects on either sides of the tower are 30° and 45°. The distance between the objects are :
-
- 180 ( 3 + √3 ) m
- 180 ( 3 - √3 ) m
- 180 ( √3 - 1 ) m
- 180 ( √3 + 1 ) m
Correct Option: D
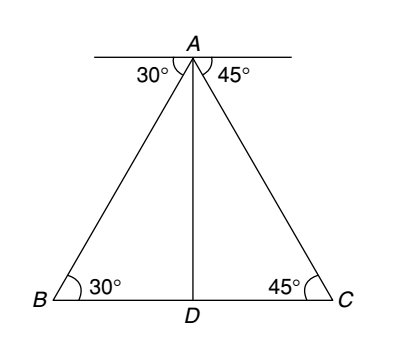
Let us draw the figure from the given question.
Let, AD be the tower and B and C be two objects.
∠ABD = 30° and ∠ACD = 45° , AD = 180 m
From ΔABD,
| tan 30° | = | AD | BD |
| ⇒ | 1 | = | 180 |
| √3 | BD |
| ⇒ | BD = | 180 √3 m |
| From ΔADC, |
| tan 45° | = | AD | DC |
| ⇒ | 1 = | 180 | ⇒ | DC = 180 m | DC |
| ∴ | BC = | BD + DC = | 180 + 180√3 |
| BC = 180 ( √3 + 1 ) m |