-
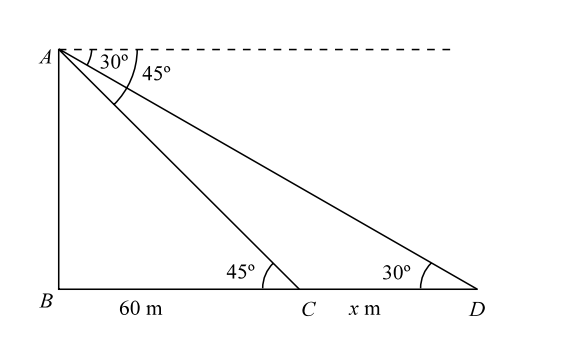
A man is watching from the top of a tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man’s eye when at a distance of 60 meter from the tower. After 5 second, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming it is running in still water?
-
- 32 Km/h
- 42 Km/h
- 38 Km/h
- 36 Km/h
- 40 Km/h
Correct Option: A
Let us draw the figure from the given question.
Given :- time = 5 seconds
| In triangle ACB , tan 45° | = | AB | ⇒ | AB = 60 m | ....... ( 1 ) |
| 60 |
| In triangle ADB , tan30° | = | , or, | AB = | ( 60 + x ) | ....... ( 2 ) | ||
| 60 + x | √3 |
| From Equation (1) and Equation (2), 60 + x = 60 √3 |
| ⇒ | x = 60 ( √3 - 1 ) | = 43.92 m | ( Putting √3 = 1.732 ) |
| ∴ Speed of the boat = | Distance ( CD ) |
| Time |
| Speed of the boat | = | 43.92 | m/s = | 43.92 | x | 18 | = 32 Km/h. |