If a flag staff of 6 m height placed on the top of a tower

Home » Aptitude » Height and Distance » Question

If a flag staff of 6 m height placed on the top of a tower throws a shadow of 2 √3 m along the ground, then the angle that the sun makes with the ground is :

1. 60°
2. 30°
3. 45°
4. None of these

Correct Option: A

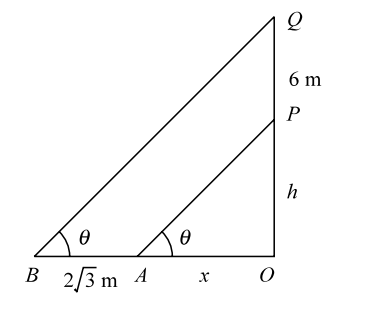
Let us draw the figure from the given question.
Let, OP be the tower of height h m and PQ be the flagstaff of height 6m. Let, the sun make an angle θ with the ground. Let, OA = x and AB = 2 √3 be the shadows of the tower and the flagstaff, respectively.

In triangle OAP , tanθ =	OP
	OA

⇒ tanθ	=	h	............ ( 1 )
		x

Also, In triangle OBQ , tanθ =	OQ
	OB

⇒	h + 6	= tanθ	............ ( 2 )
	x + 2√3

From equations ( 1 ) and ( 2 ) , we get

∴	h	=	h + 6	⇒	hx + 2√3 h	= hx + 6x
	x		x + 2√3

⇒

2√3h

⇒	h	=	6	=	√3
	x		2√3

⇒

tan θ = √3 = tan60°

⇒

θ = 60° .