Area and Perimeter
Area
Area of any particular figure is the space enclosed by the boundary of that figure in 2- dimension plane.
Unit of an area = square unit
Perimeter
Total length of the boundary of any enclosed figure is called perimeter.
Triangle
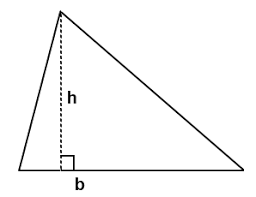
A triangle is a polygon with three line segments.
or, A closed figure which is made of three line segments. It has three edges and three vertices.
| Area = | × Base × Height | |
| 2 |
| Perimeter = sum of all three sides |
Example: Find the area of a triangle whose base is 12 cm and height is 7 cm.
Solution:-given, base=12 cm height=7 cm
area=?
| Area = | × Base × Height | |
| 2 |
| Area = | × 12 × 7 | |
| 2 |
= 6 × 7
= 42 cm2
Example- Find the perimeter of a triangle whose sides are 3 cm, 4 cm and 5 cm.
Solution:- given, sides are 3 cm, 4 cm and 5 cm Perimeter = sum of all three sides = 3 + 4 + 5 = 12 cm
Types of Triangle
Equilateral Triangle

A triangle in which all three sides are equal and each angle is 60 degree.
| Area = | × (side)² | |
| 4 |
| Perimeter = 3 × side |
Example-Find the area and perimeter of an equilateral triangle , whose sides are 14 cm long.
Solution:- given, side = 14 cm
area=?
perimeter =?
| Area = | × (side)² | |
| 4 |
| Area = | × (14)² | |
| 4 |
| Area = | × 196 | |
| 4 |
= √3 × 49
= 49√3 cm2
Perimeter = 3 × side
= 3 × 14
= 42 cm
Isosceles Triangle

A triangle in which two sides are equal is called isosceles triangle.
Let equal sides = a
other side = b
| Area = | × √(4a² + b²) | |
| 4 |
| Perimeter = a + a + b = 2a + b |
Example- Find the area and perimeter of an isosceles triangle whose equal sides 3 cm and other side 4 cm.
Solution:- Let a = 3 and b = 4 cm
| Area = | × √(4a² + b²) | |
| 4 |
| = | × √(4 × 3² - 4²) | |
| 4 |
= √( 4×9 - 16 )
= √( 36 - 16 )
= √20
= √4 × 5
= 2 √ 5 cm²
Perimeter = sum of all three sides
= 3 + 3 + 4
= 10 cm
Scalene Triangle

A triangle in which all three sides are different.
| Area = s√(s- a) (s- b) (s- c) |
where- a,b&c are sides and s is semi-perimeter
| s = | |
| 2 |
| Perimeter = a + b + c |
Example- Find the area and perimeter of a triangle whose sides are 9 cm, 12 cm and 7 cm.
Solution:-
Let a = 9 cm , b = 12 cm and c = 7 cm
| s = | |
| 2 |
| s = | |
| 2 |
| = | |
| 2 |
= 14
( s - a ) = ( 14 - 9 ) = 5
( s - b ) = ( 14 - 12 ) = 2
( s - c ) = ( 14 - 7 ) = 7
Area = √s (s- a ) ( s- b ) ( s- c)
= √14 × 5 × 2 ×7
= 14 × 5 × 14
= 14 × 2.23
= 31.22 cm2
Perimeter = ( a + b + c )
= 9 + 12 + 7
= 28 cm
Properties of Triangle
1.In a triangle, sum of any two sides is greater than the third side.
2. In a triangle, difference of any two side is less than the third side.
3. In a triangle, sum of all three angles is 180°( angle sum property ).
4. In a triangle, side opposite to the largest angle is the longest side.
5. In a triangle, an exterior angle is the sum of its opposite interior angles ( exterior angle property ).
6. The median of a triangle divides it into two triangles of equal areas.
Rectangle
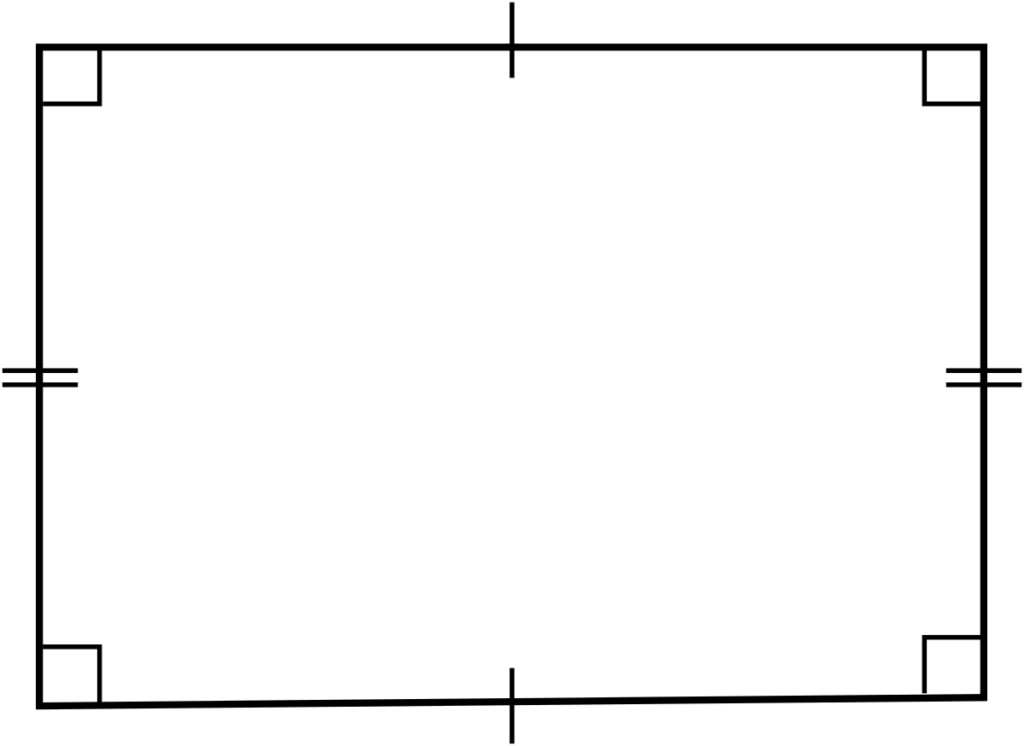
Rectangle is a four sided polygon in which
a. Pairs of opposite sides are equal and parallel.
b. Each angle measure 90 degree.
c. Diagonals equal and bisect each other.
All rectangles are parallelogram but all parallelograms is not rectangle
| Area = Length × Breadth |
| Length = | |
| Breadth |
| Breadth = | |
| Length |
| Perimeter = 2 (Length + Breadth) |
| Diagonal = √L² + B² |
Ex-Find the area and perimeter of a rectangle whose length 42 cm and breadth 35 cm. Solution:- given Length = 42 cm
Breadth = 35 cm
Area = Length × Breadth
= 42 × 35
= 1470 cm2
Ex- Find the area and perimeter of a rectangle one of whose sides is 8 cm and diagonal 10 cm.
Solution:-
given, one side = 8 cm
diagonal = 10 cm
Diagonal = √( L² + B²)
or, 10 = √( 8² + b²)
Squaring on both sides
or, 10² = (√8² + b²)²
or, 100 = 82 + b2
or, 100 = 64 + b2
or, 100 - 64 = b2
or, b2 = 36
or, b = √36
or, b = 6
Hence, other side = 6 cm
Now, Area = Length × Breadth
= 8 × 6
= 48 cm2
And, Perimeter = 2 ( Length + Breadth )
= 2 ( 8 + 6 )
= 2 × 14
= 28 cm
Square

Square is a four sided polygon in which
a. all sides are equal.
b. Each internal angle is 90 degree.
c. Diagonals equal and bisect each other at right angle.
All square are rhombus but all rhombus are not square.
| Area = (side)² = | × (Diagonal)² | |
| 2 |
| Perimeter = 4 × side |
| Diagonal = √2 × side |
Example- Find the area and perimeter of a square whose each side is 35 cm.
Solution:- given, side = 35 cm
Area = ( side ) 2
= ( 35 ) 2
= 1225 cm 2
Perimeter = 4 × side
= 4 × 35
= 140 cm
Example- Find the area of a square the length of whose diagonal is 24 cm.
Solution:- given, diagonal = 24 cm
| = | (Diagonal)² | |
| 2 |
| = | (24)² | |
| 2 |
| = | ×576 | |
| 2 |
= 288 cm2
Parallelogram
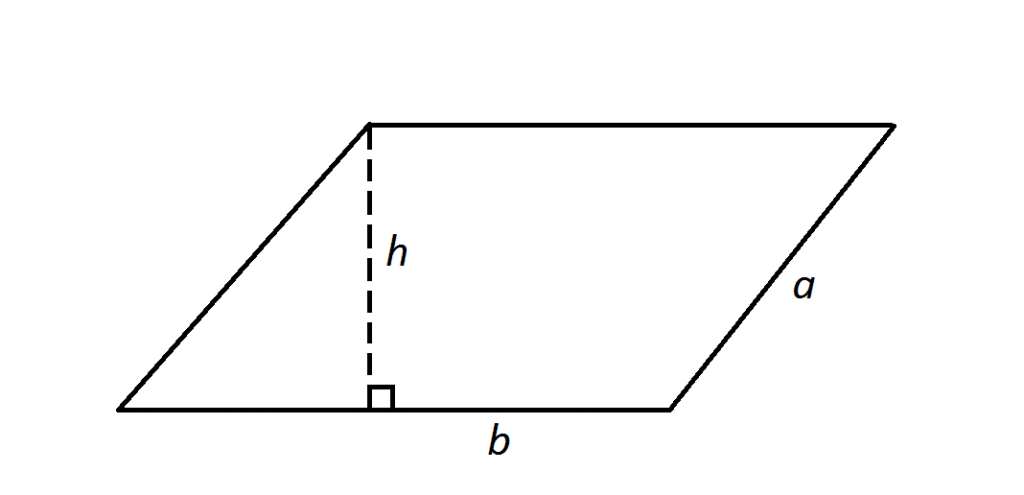
A Parallelogram is a quadrilateral in which
a. Opposite sides are parallel and equal.
b. Opposite angles are equal
c. Diagonals bisect each other.
Each diagonal of a parallelogram divides it into two triangles of equal area.
A parallelogram and a rectangle have equal areas if they are on the same base and between the same parallel lines.
| Area = Base × Height |
| Perimeter = 2 ×( Length + Breadth ) |
Example- Find the area and perimeter of a parallelogram whose base is 19 cm and height is 7 cm.
Solution:-
given, base = 19 cm
height= 7 cm
Area = Base × Height
= 19 × 7
= 133 cm2
Rhombus

A Rhombus is a quadrilateral in which all sides are equal.
a. Length of diagonals are different.
b. Diagonals bisect each other at right angle.
c. opposite angles are equal.
| Area = Base × Height |
| Area = | × Product of diagonals = | × d1 × d2 | ||
| 2 | 2 |
| Perimeter of rhombus = 4 × Side |
Example- Find the area a rhombus whose diagonals are 8 cm and 10 cm.
Solution:-
given, first diagonal = 8 cm
other diagonal = 10 cm
| Area = | × d1 × d2 = | × 8 × 10 | ||
| 2 | 2 |
= 40 cm2
Example- Find the perimeter of rhombus whose diagonals are 12 cm and 16 cm.
Solution:-
Let ABCD is a rhombus in which AC = 12 cm and BD = 16 cm.
We know that, the diagonal of rhombus bisect each other at 90 degree.
Let AC and BD bisect at O.
then, triangle AOB is a right angle triangle in which
OA = 12/2 = 6 cm and OB = 16/2 = 8 cm
Now, in triangle AOB
by pythagoras theorem
AB2 = OA2 + OB2
or, AB2 = 62 + 82
or, AB2 = 36 + 64
or, AB2 = 100
then AB = √100
= 10 cm
AB = BC = CD= DA = 10 cm
∴ Perimeter = 4 × side
= 4 × 10
= 40 cm
Trapezium
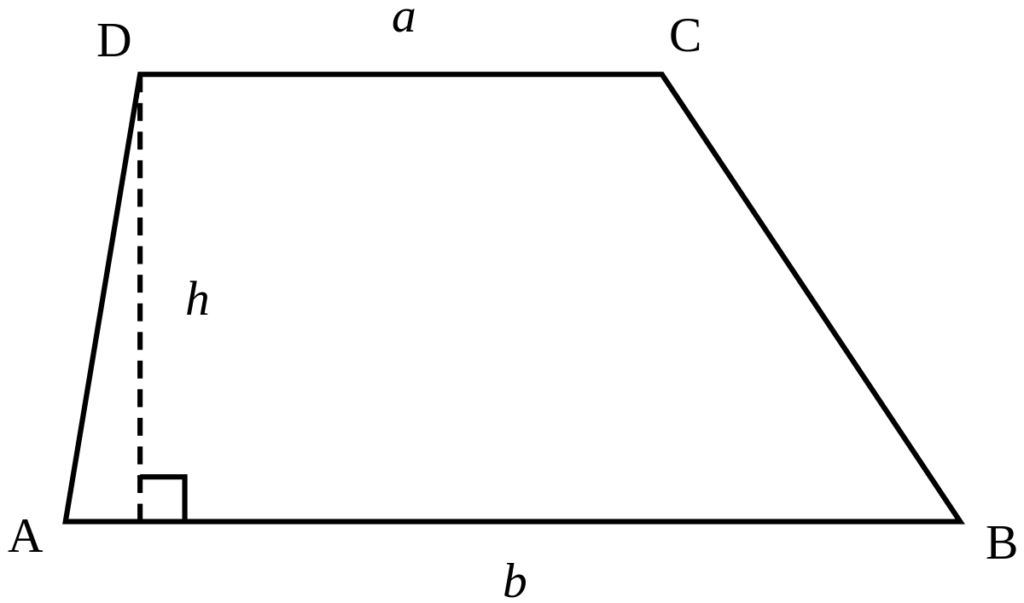
A Trapezium is a quadrilateral in which one pair of opposite sides are parallel.
| Area = | × (sum of parallel sides)×(Distance between parallel sides ) | |
| 2 |
| Perimeter = Sum of all sides |
Example- Find the area of trapezium whose parallel sides are 35 cm and 45 cm and distance between parallel sides is 9 cm.
Solution:-
given, parallel sides = 35 cm and 45 cm
and distance = 9 cm
| Area = | × (sum of parallel sides)×(Distance between parallel sides ) | |
| 2 |
| = | × (35) × 9 | |
| 2 |
| = | × 80 × 9 | |
| 2 |
| = 40 × 9 |
= 360 cm²
| Area of 4 walls of a room = 2 × ( Length + Breadth ) × Height |
| Area of 4 walls of a room = Perimeter of room × Height |
Example- Area of four walls of a room is 272 sq. meters. The breadth and height of the room are 6 m and 8 m respectively.Find the length of the room.
Solution:-
given, Area = 272 sq.m
breadth = 6 m
height = 8 m
| Area of 4 walls of a room = 2 × ( Length + Breadth ) × Height |
| or, 272 = 2 × (Length + 6 ) × 8 |
or, 272 = 16 × ( Length + 6 )
or, 272 ÷ 16 = Length + 6
or, 17 = Length + 6
or, Length = 17 - 6
then, Length = 11 cm
Polygon
A polygon is a figure enclosed by three or more than three line segments.
Examples of polygons are- triangle,quadrilateral,pentagon,hexagon etc.
Regular Polygon:- A polygon in which all sides are equal is called regular polygon.
For example- regular pentagon, regular hexagon etc.
Property of polygon
| Sum of all interior angles of a polygon = (n - 2) × 180° |
Where, n = number of sides
Example- Find the sum of all interior angles of a pentagon.
Solution:- Here, n = 5
∴ Sum of all interior angles of a pentagon
= ( n - 2 ) × 180°
= ( 5 - 2 ) × 180°
= 3 × 180°
= 540°
| Each interior angle of a regular polygon = | × 180° | |
| 2 |
Example- Find the each interior angle of a regular hexagon.
Solution:- Here, n = 6
| Each interior angle of a regular polygon = | × 180° | |
| 2 |
| = | × 180° | |
| 6 |
| = | × 180° | |
| 6 |
= 4 × 30°
= 120 °
| Sum of all exterior angles of a polygon = 360° |
| Each exterior angle of regular a polygon = | |
| n |
Example- Find each exterior angle of a regular pentagon.
Solution:-
Here, n = 5
| Each exterior angle of a regular polygon = | |
| n |
= 360°/5
= 72°
| Number of diagonals in a polygon = n | |
| 2 |
Example- Find number of diagonals in hexagon.
Solution:-
Here, n = 6
| Number of diagonals in a polygon = n | |
| = 6 | |
| 2 |
= 3 × 3
= 9
Regular Pentagon
A polygon which has five sides and five vertices and all sides are equal in length.
| Area of regular pentagon = | × 5a | |
| 4 |
Where, a = Length of side
Perimeter = 5 × side = 5a
Regular Hexagon
A polygon which has six sides and six vertices and all the sides and angles are equal.
| Area of regular hexagon = | × 6a | |
| 4 |
Perimeter = 6 × side = 6a
where, a = Length of side
Example- Find the area and perimeter of a regular hexagon whose side is 12 cm.
Solution:- given, a = 12 cm
| Area of regular hexagon = | √3 | × 6a² |
| 100 |
| Area of regular hexagon = | √3 | × 6(12)² |
| 100 |
| Area of regular hexagon = | √3 | × 6 × 144 |
| 100 |
= 216 √3 cm²
Perimeter = 6a
= 6 × 12
= 72 cm
Regular Octagon
A polygon which has eight sides and eight vertices and all sides and angles are equal.
| Area of regular octagon = | 2 (√2 + 1) a² |
| Perimeter = 8 × side = 8a |
Circle
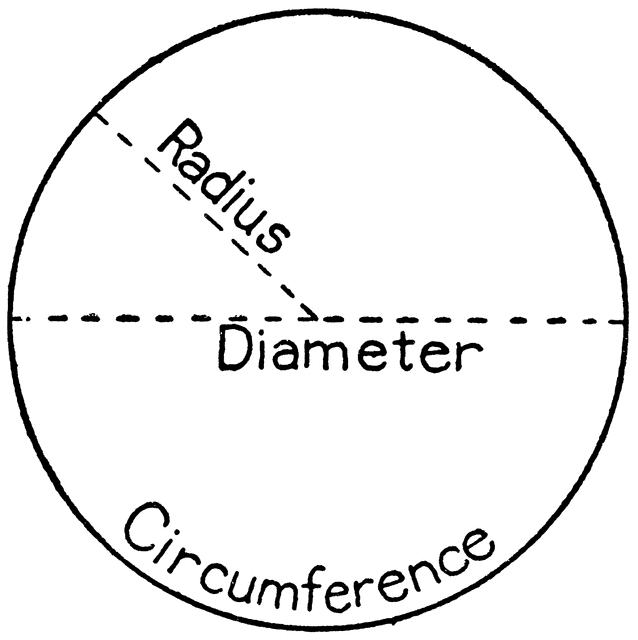
A circle is a closed figure which is the set of points in a plane from the center where the distance between center to the circle is constant.
| Area = πr² |
| Diameter = 2r |
| Radius = | D |
| 2 |
Where, r = radius of the circle,
D = diameter and π = 22/7 or 3.14
Example- Find the area of a circle whose radius is 7 cm.
Solution:-
given, radius = 7 cm
| Area = πr² |
| = | 22 | × (7)² |
| 7 |
| = | 22 | × 7 × 7 |
| 7 |
= 154 cm2
Circumference of a circle
Circumference of a circle is the length of the boundary of a circle. It is also called as perimeter of circle.
| Circumference = 2πr = πd |
Example- Find the circumference of a circle whose radius 42 m.
Solution:-
given, radius = 42 cm
Circumference = 2πr
| = 2 × | 22 | × 42 |
| 7 |
= 22 × 2 × 6 = 44 × 6 = 264 cm
Length of Arc
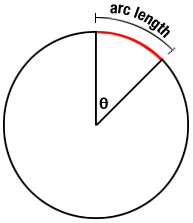
Length of circumference which is enclosed by two radii .
| Length of arc (l) = | θ | × 2πr = | θ | × πr |
| 360° | 180° |
where θ = angle between two radii
Sector

Sector is plane enclosed between two radii.
| Area of sector = | × πr | |
| 360° |
Segment
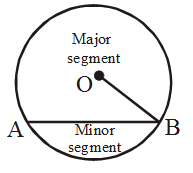
Region which is enclosed by a chord and circumference of a circle.
| Area of segment = Area of sector - Area of triangle |
Semi-circle

The diameter divide the circle into two semi-circles.
| Area = | |
| 2 |
| Perimeter of curve part = πr |
| Perimeter of semi-circle = πr + Diameter = πr + D = πr + 2r |
Example- Find the area of semi-circle whose radius is 7 cm.
Solution:-
given, radius = 7 cm
| Area = | |
| 2 |
| = | × 7 × 7 | |
| 7 |
| = | 49 | |
| 7 |
= 154/2
= 77 cm²
Example- The diameter of a wheel is 49 cm.Find the distance traveled by the wheel in 200 revolutions.
Solution:-
given, diameter = 49 cm
number of revolutions = 200
Distance traveled in 1 revolutions = circumference of circle = πd
= ( 22/7 ) × 49
= 22 × 7
= 154 cm
Distance traveled in 200 revolutions = Circumference × No. of Revolutions = 154 ×200
= 30800 cm
= 308 m
Circular Ring
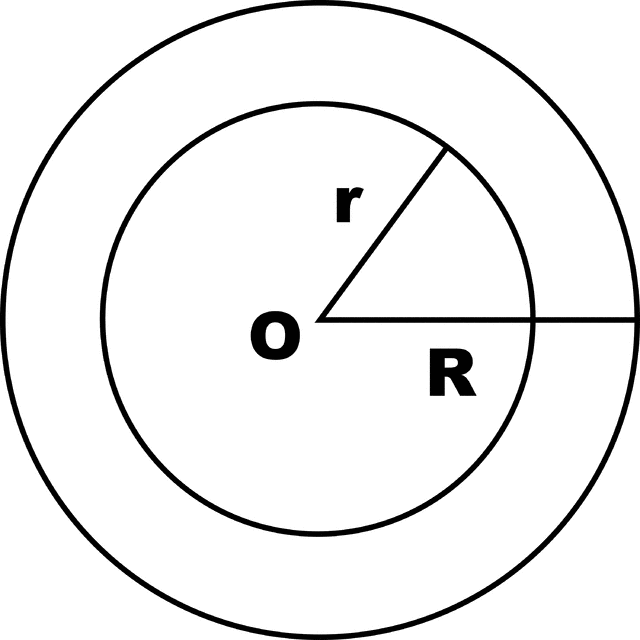
A plane figure enclosed by the circumference of two concentric circles of different radii.
| Area = Area of outer circle - Area of inner circle |
| Area = πR² - πr² |
| Area = πR² - πr² | = π(R + r) (R - r) |
| Circumference = 2πR - 2πr = 2π ( R - r ) |
where, R = radius of outer circle
r = radius of inner circle
Example- Find the radius of the outer circle whose inner circumference is 440 m and wide of the circular race track is 16 m.
Solution:-
given, Inner circumference = 440 m
wide of circular race track = 16 m
Inner circumference = 440
2πr = 440
| or, 2 × | × r = 440 | |
| 7 |
| or, | × r = 440 | |
| 7 |
| or, r = | × 7 | |
| 44 |
∴ r = 70 m
Wide of circular race track = 16 m
or, ( R - r ) = 16
or, R - 70 = 16
or, R = 16 + 70
then, R = 86 m