Surface area related to the amount of space covering the outside of a three-dimensional shape.
Volume and surface area are related to bodies which is solids or hollow.
these bodies occupy space and have generally three dimensions length,breadth and height.

Surface Area

Surface area is the region covered by the closed plane figure.surface area of a plane figure is the area of all of its surfaces together.It is measured in square unit for example square meter,square centimeter etc.

Lateral or curved surface area

Area of solid without its top and bottom is called lateral or curved surface area.

Total surface area

Total surface area is the area of whole surface of any object including the area of base and area of top.

Volume

Volume is the space occupied by an object is called the volume of that particular object.
It is measured in cube unit like cubic centimeter, cubic meter etc.

Cube

A three dimensional figure having 6 square faces, 8 vertices and 12 edges with equal length, breadth and height is called cube.

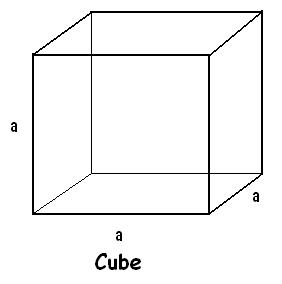
1.Lateral surface area = Perimeter of base × Height
= 4a × a
L.S.A = 4a²

2.Total surface area = Lateral surface area + area of top and area of bottom
= 4a² + 2a²
T.S.A = 6a²

3.Diagonal = √3a

4.Perimeter = 12a

5. Volume = Area of base × Height
= a² × a
Volume = a³
Where, a = side of cube

Ex- The diagonal of a cube is 9√3 cm. Find its lateral surface area and volume.
Solution:- Let the side of cube = a
given, Diagonal = 9√3 cm.
lateral surface area and volume = ?
According to question,
Diagonal = 9√3 cm.
or, √3a = 9√3 or, a = 9√3 /√3 = 9
∴ Lateral surface area = 4a²
= 4 ( 9 )²
= 4 × 9 × 9
= 324 sq cm
∴ Volume = a³
= ( 9 )³
= 9 × 9 × 9
= 729 cm ³

Cuboid

A three dimensional figure having 6 rectangular faces, 8 vertices and 12 edges with different length breadth and height.
Let Length = l
breadth = b
height = h

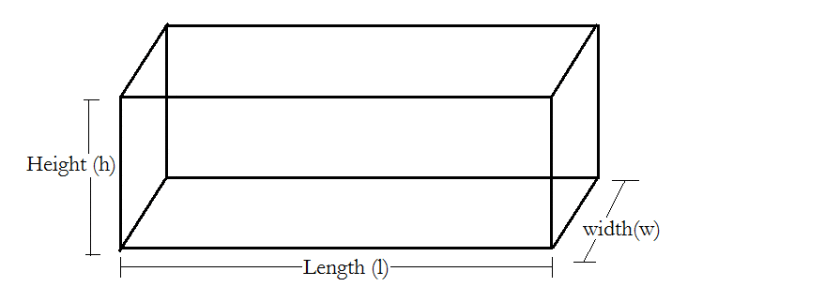
1.Lateral surface area = Perimeter of base × height
= 2 ( l + b ) × h
LSA = 2 ( l + b ) h
2. Total surface area = Lateral surface area + area of top and bottom
= 2 ( l + b ) h + 2lb
= 2lh + 2bh + 2lb
= 2 ( lh + bh + lb )
TSA = 2 ( lb + bh + lh )
3. Diagonal = √ ( l ² + b² + h² )
4. Perimeter = 4 ( l + b + h )
5. Volume = Area of base × Height
= ( l × b ) × h
= l × b × h
Volume = lbh

Ex- Find the volume and surface area of a cuboid 17 m long, 13 m broad and 5 m height.
Solution:- given Length = 17 m
breadth = 13 m
height = 6 m
Volume = lbh
= 17 × 13 × 6
= 1326 m ³
Surface area = 2 ( lb + bh + lh )
= 2 ( 17 × 13 + 13 × 6 + 6 × 17 )
= 2 ( 121 + 78 + 102 )
= 2 × 301
= 602 sq m

Ex- A wooden box measures 12 cm × 8 cm × 7 cm. Thickness of wood is 1.5 cm. Find the volume of the wood required to make the box.
Solution:- given, External length = 12 cm
breadth = 8 cm
height = 7 cm
External volume = Length × Breadth × Height
= 12 × 8 × 7
= 672 cm ³
Internal length = 12 - ( 2 × 1.5 ) = 9 cm
breadth = 8 - ( 2 × 1.5 ) = 5 cm
height = 7 - ( 2 × 1.5 ) = 4 cm Internal volume =Length × Breadth × Height
= 9 × 5 × 4
= 180 cm ³
∴ Volume of wood = External volume - Internal volume = 672 - 180
= 492 cm ³

Ex- Find the length of the largest pole that can be placed in a room 12 m long, 8 m broad and 10 m height.
Solution:- given, Length = 12 m
breadth = 8 m
height = 10 m
Length of the longest pole = Length of the diagonal
= √ ( l ² + b² + h² )
= √ ( 12² + 8² + 10² )
= √( 144 + 64 + 100 ) = √308
= 4√77 m

Cylinder

A cylinder is a three dimensional shape with circular shapes at top and base and two parallel lines connecting the circular ends.

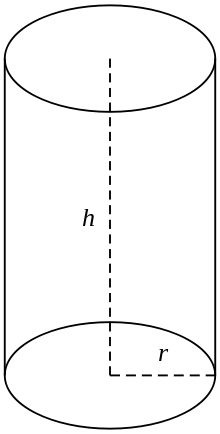
1.Curved surface area = Perimeter of base × Height
= 2πr × h
CSA = 2πrh 2. Total surface area = Curved surface area + Area of top and base
= 2πrh + 2πr ²
TSA = 2πr ( r + h )
3. Volume = Area of base × Height
= πr ² × h
V = πr ²h
Where, r = radius of the cylinder
h = height of the cylinder

Hollow Cylinder

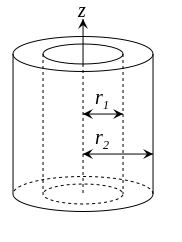
1.Curved surface area = Curved surface area of outer surface + curved surface area of inner surface
= 2πRh + 2πrh
CSA = 2πh ( R + r )
2. Total surface area = Curved surface area + Area of top and base
= 2πh ( R + r ) + 2π ( R² - r ² ) TSA = 2πh ( R + r ) + 2π ( R + r ) ( R - r )
3. Volume = Volume of outer cylinder - Volume of inner cylinder
= πR ²h - πr ²h
= πh ( R ² - r ² )
V = πh ( R + r ) ( R - r )

Ex- Find the volume, curved surface area and the total surface area of a cylinder with base radius of 7 cm and height 50 cm.
Solution:- given, radius = 7 cm
height = 50 cm
Volume = πr²h
= ( 22/7 ) × 7² × 50
= ( 22/7 ) × 7 × 7 × 50
= 22 × 7 × 50
= 7700 cm ³
Curved surface area = 2πrh
= 2 × ( 22/7 ) × 7 × 50
= 2 × 22 × 50
= 2200 cm²
Total surface area = 2πr ( r + h )
= 2 × ( 22/7 ) × 7 ( 7 + 50 )
= 2 × 22 × 57
= 2508 cm ²

Ex- A hollow cylinder made of wood has thickness 2 cm while its external radius is 5 cm. if the height of the cylinder is 10 cm,then find the volume and curved surface area of the cylinder.
Solution:- given, R = 5 cm
thickness of wood = 2 cm
height = 10 cm
inner radius = outer radius - thickness
r = 5 - 2
∴ r = 3 cm
Volume of wood = πh ( R ² - r ² )
= ( 22/7 ) × 10 ( 5² - 3² )
= ( 220/7 ) × ( 25 - 9 )
= ( 220/7 ) × 16
= 1452/7 cm³

Cone

A three dimensional figure having one circular base and one vertex. It is solid or hollow. It is formed by the rotation of a triangle along any of the side.

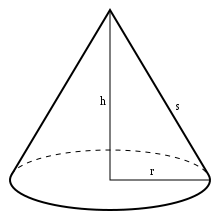
1.Slant height ( l ) = √( r ² + h ²  )
2. Curved surface area = πrl = πr√( r ² + h ² )
3. Total surface Area = curved surface area + Area of base
= πrl + πr ²
TSA = πr ( l + r )
4. Volume = ( 1/3 ) × Base Area × Height
V = ( 1/3 ) × πr ² × h
Where , r = radius of base
h = height of the cone
l = slant height

Ex- The curved surface area of a right circular cone of radius 14 cm is 440 sq cm. Find the slant height of the cone.
Solution:- given, radius = 14 cm
curved surface area = 440 sq cm
curved surface area = 440
or, πrl = 440
or, ( 22/7 ) × 14 × l = 440
or, 44 &time;s l = 440
or, l = 440/44
∴ l = 10 cm

Ex- The base radius and height of a cone are 7 cm and 24 cm respectively. Find whole surface area and volume of the cone.
Solution:- given, radius = 7 cm
Height = 24 cm
l = √( r² + h² )
= √( 7 ² + 24 ² )
= √( 49 + 576 ) = √ 625
∴ l = 25 cm
Total surface area = πr ( l + r )
= ( 22/7 ) × 7 ( 25 + 7 )
= 22 × 32
= 704 cm²
Volume = ( 1/3 ) × πr² × h
= ( 1/3 ) &time;s ( 22/7 ) × 7² × 24
= 22 × 7 × 8
= 1232 cm ³

Frustum of cone

If the part of solid such as cone or pyramid cut by a plane parallel to the base so as to divide the cone into two parts upper part and lower part, then the lower part is called frustum.

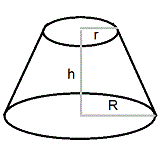
Slant height ( l ) = √{ h² + ( R - r )² }
Curved surface area = π ( R + r )l
= π ( R + r )√{ h² + ( R - r )² }
Total surface area = π{ rl + Rl + r² + R² } Volume = ( rh/3 ) × ( r² + R² + rR )
where, r = radius of top
R = radius of base
h = Height
l = slant height

Ex- The a frustum of a right circular cone has a radius of base and top 5 cm and 3 cm respectively and a height of 21 cm. Find the area of its whole surface and volume.
Solution:- given, R = 5 cm
r = 3 cm
h = 21 cm
l = √{ h² + ( R - r )² }
= √ { 21² + ( 5 - 3 )² }
= √( 441 + 4 )
= √445
= 21.01 (approx.)
Total surface area = π{ ( rl + Rl ) + r² + R² } = ( 22/7 ) × { ( 3 × 21.01 + 5 × 21.01 ) + 3² + 5² } = ( 22/7 ) × { 63.03 + 105.05 + 9 + 25 }
= ( 22/7 ) × 202
= 22 × 29
= 638 cm²
Volume = ( πh/3 ) × ( r² + R² + rR )
= ( 22/7 ) × ( 21/3 ) × ( 3² + 5² + 3 × 5 )
= ( 22/7 ) × 7 × (9 + 25 + 15 )
= ( 22/7 ) × 7 × 49
= ( 1/3 ) × 7 × 22
= 22 × 21 × 49
= 22638 cm ³

Ex- The frustum of a right circular cone has the diameters of base 20 cm, of top 12 cm and height of 10 cm. Find its slant height.
Solution:- given, diameter of base = 20 cm R = 20/2 = 10 cm
diameter of top = 12 cm r = 12/2 = 6 cm
height = 10 cm
Slant height ( l ) = √{ h² + ( R - r )² }
= √{ 10² + ( 10 - 6 )² }
= √{ 100 + 4² }
= √{ 100 + 16 } = √ 4 × 29
= 2√ 29 cm

Sphere

A three-dimensional solid figure, all points of which are equidistant from a fixed point. That fixed point is center and constant distance is radius of the sphere.

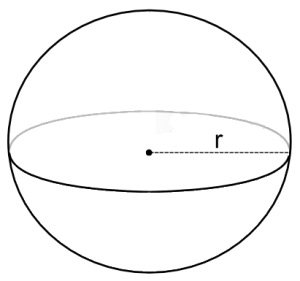
Surface area = 4 πr²
Volume = ( 4/3 ) × πr³
Where, r = radius of the sphere

Ex- Find the volume of sphere of diameter 42 cm.
Solution:- given, diameter = 42 cm
radius = 42/2 = 21 cm
Volume = ( 4/3 ) × πr³
= ( 4/3 ) × ( 22/7 ) × ( 21 )³
= 4 × 22 × 21 × 21
= 88 × 441
= 38808 cm³

Ex- Find the surface area of a sphere of radius 7 cm.
Solution:- given, radius = 7 cm
Area = 4 πr²
= 4 × ( 22/7 ) × ( 7 )²
= 4 × 22 × 7
= 88 × 7
= 616 cm²

Hollow Sphere

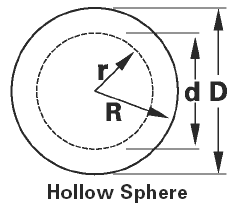
Internal surface area = 4 πr²
External surface area = 4 πR²
Volume = External volume - Internal volume
= ( 4/3 )>πR³ - ( 4/3 )>πr³
V = ( 4/3 )π ( R³ - r³ )
where, R = External radius
r = Internal radius

Ex- Find the volume of hollow sphere whose outer and inner radius is 4 cm and 2 cm respectively.
Solution:- given, R = 4 cm
r = 2 cm
V = ( 4 π/3 )( R³ - r³ )
= ( 4/3 )× ( 22/7 ) ( 4³ - 2³ )
= ( 88/21 )× ( 64 - 27 )
= ( 88/21 )× 37
= 234.66 cm³

Hemisphere

Hemisphere is the half part of a sphere. when sphere divide into two equal half each half is called hemisphere.

Curved surface area = 2 πr²
Total surface area = 3 πr²
Volume = ( 2πr³ ) / 3
Where, r = radius of the sphere

Ex- Find the curved surface area, total surface area and volume of a hemisphere of radius 42 cm.
Solution:- given, radius = 42 cm
Curved surface area = 2 πr²
= 2 × ( 22/7 ) × 42²
= 2 × 22 × 42 × 6
= 11088 cm²
Total surface area = 3 πr²
= 3 × ( 22/7 ) 42²
= 3 × 22 × 42 ×6
= 16632 cm²
Total surface area = 3 πr²
= 3 × ( 22/7 ) 42²
= 3 × 22 × 42 ×6
= 16632 cm²
Volume = ( 2πr³ ) / 3
= ( 2 × 22 × 42³ ) / ( 3 × 7 )
= 2 × 22 × 2 × 42 × 42
= 155232 cm³

Prism

A three-dimensional figure whose top and base are equal and parallel to each other. whose sides are parallelograms.

1.Lateral surface area = Perimeter of base × Height of prism
2. Total surface area of prism = Lateral surface area + Area of base and top 3. Volume = Area of base × Height

Ex- The base of right prism is a square having side 12 cm. It its height is 9 cm. Find the surface area, total surface area and volume of the prism. Solution:- given, side = 12 cm
height = 9 cm
Lateral surface area = Perimeter of base × Height
= ( 4 × 12 ) × 9
= 432 cm²
Total surface area = Lateral surface area + area of base and top
= 432 + 2 × Area of square
= 432 + 2 × 12²
= 432 + 2 × 144
= 432 + 288
= 720 cm²
Volume = Area of base × Height
= ( 12 )² × 9
= 144 × 9
= 1296 cm²

Pyramid

A solid whose base is a polygon and top is a point and whose faces are triangles is called a pyramid.

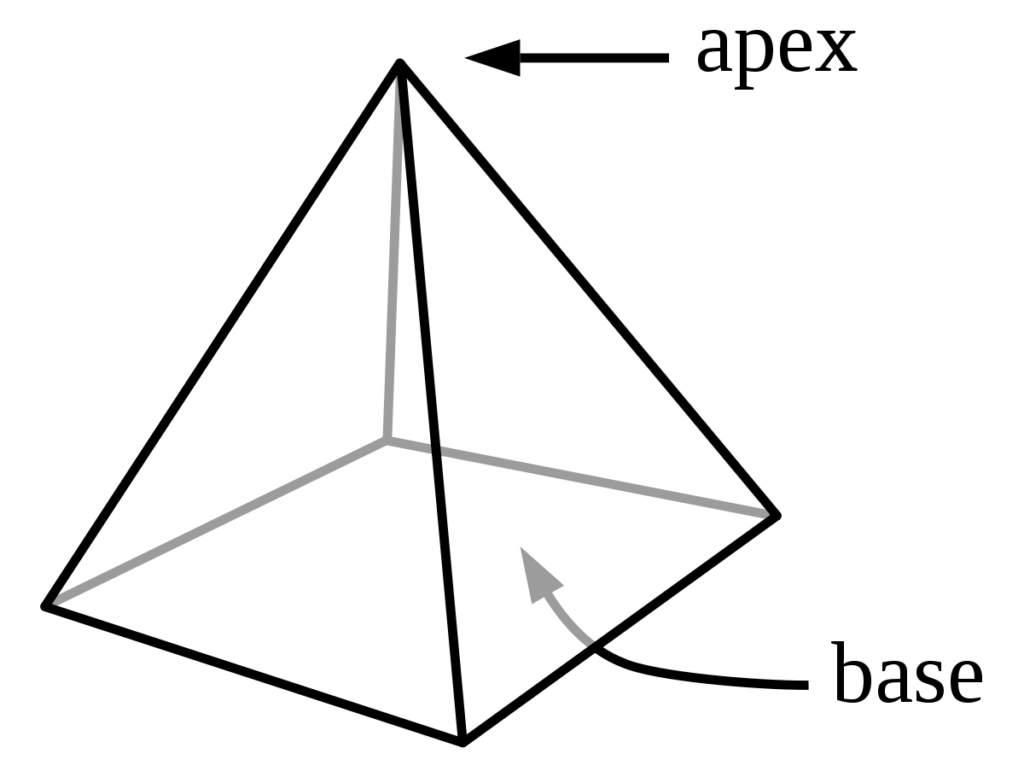
Lateral surface area = ( 1/2 ) × Perimeter of base × Slant height Total surface area = Lateral surface area + Area of the base
Volume = ( 1/3 ) × Area of base × Height

Ex- The base of a pyramid is a square whose side 8 cm, slant height 15cm and vertical height is 18 cm. Find the curved surface area, total surface are and volume of the pyramid.
Solution:- given side of square = 8 cm
slant height = 15 cm
vertical height = 18 cm
Lateral surface area = ( 1/2 ) × × Perimeter of base × Slant height
= ( 1/2 ) × × ( 4 × 8 ) × 15
= 16 × 15
= 240 cm²
Total surface area = Lateral surface area + Area of the base
= 240 + 4 × side²
= 240 + 4 × ( 8 )²
= 240 + 4 × 64
= 240 + 256
= 496 cm²
Volume = ( 1/3 ) × × Area of base × Height
= ( 1/3 ) × ( 8 × 8 ) × 18
= 64 × 6
= 384 cm²

Ex- Find the total surface area of a pyramid having a slant height of 8 cm and a base which is a square of side 4 cm.
Solution:- given, l = 8 cm
side of base = 4 cm
Lateral surface area = ( 1/2 ) × Perimeter of base × Slant height
= ( 1/2 ) × ( 4 × 4 ) × 8
= 16 × 4
= 64 cm²
Total surface area = Lateral surface area + Area of the base
= 64 + 4²
= 64 + 16
= 80 cm²