Plane Geometry

Plane Geometry

Easy Questions
Moderate Questions
Difficult Questions
Plane Geometry Tutorial

Aptitude

Simplification
Number System
Fractions
Elementary Algebra
LCM and HCF
Approximation
Unitary Method
Linear Equation
Quadratic Equation
Discount
Average
Surds and Indices
Percentage
Square root and cube root
Order of Magnitude
Work and Wages
Odd Man Out and Series
Algebra
Profit and Loss
Stocks and Shares
True Discount
Ratio, Proportion
Partnership
Alligation or Mixture
Time and Work
Pipes and Cistern
Speed, Time and Distance
Problem on Trains
Height and Distance
Banker's Discount
Boats and Streams
Races and games
Problems on Ages
Clocks and Calendars
Simple interest
Compound Interest
Sets and Functions
Area and Perimeter
Volume and Surface Area of Solid Figures
Sequences and Series
Plane Geometry
Logarithm
Probability
Permutation and Combination
Statistics
Mensuration
Trigonometry
Aptitude miscellaneous
  1. If the bisector of an angle of Δ bisects the opposite side, then the Δ is :










  1. View Hint View Answer Discuss in Forum

    According to given question, ∠1 = ∠2

    ∴AB = BD
    ACAD


    Correct Option: B

    Since ∠1 = ∠2

    ∴AB = BD
    ACAD

    But BD = CD (given)
    ∴AB = 1
    AC

    AB = AC
    ∴ the given ∆ is isosceles


  1. The areas of two similar Δs are 81 cm2 and 144 cm2. If the largest side of the smaller Δ is 27 cm, then the largest side of the larger Δ is :












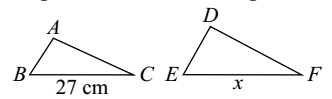
  1. View Hint View Answer Discuss in Forum

    Let ABC and DEF be the two similar Δs having area 81 cm2 and 144 cm2 respectively:
    Let BC = 27 cm
    Then since ΔABC ∼ ΔDEF

    ∴area (∆ABC) = BC2(area Theorem)
    area (∆DEF)EF2

    Correct Option: C

    Let ABC and DEF be the two similar Δs having area 81 cm2 and 144 cm2 respectively:
    Let BC = 27 cm
    Then since ΔABC ∼ ΔDEF

    ∴ar (∆ABC) = BC2(area Theorem)
    ar(∆DEF)EF2

    81 = (27)2⇒9 = 27
    144x212x

    ∴ x = 36 cm.

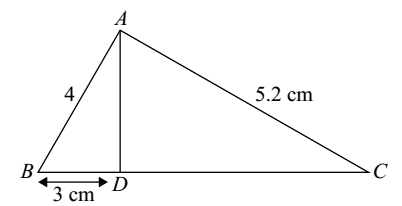
  1. In the given figure ∠BAD = ∠CAD. AB = 4 cm, AC = 5.2 cm, BD = 3 cm. Find BC.












  1. View Hint View Answer Discuss in Forum

    According to question, Given that
    ∠BAD = ∠CAD. AB = 4 cm, AC = 5.2 cm, BD = 3 cm
    In ΔABC, AD is the bisector of ∠A

    AB=BD(Internal bisector prop.)
    ACCD

    Correct Option: A

    According to question, Given that
    ∠BAD = ∠CAD. AB = 4 cm, AC = 5.2 cm, BD = 3 cm
    In ΔABC, AD is the bisector of ∠A

    AB=BD(Internal bisector prop.)
    ACCD

    4=3⇒ DC = 3.9 cm
    5.2DC

    But BC = BD + CD = 3cm + 3.9 cm = 6.9 cm

  1. A ladder 15 m long reaches a window which is 9 m above the ground on one side of street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 12 m high. What is the width of the street:










  1. View Hint View Answer Discuss in Forum

    Draw a figure as per given question,
    In a Right triangle ADC, Use the (Pythagoras Theorem)
    AC = √DC2 - AD2

    In a Right triangle BCE, Use the (Pythagoras Theorem)
    CB = √ CD2 - BE2



    Correct Option: D

    Draw a figure as per given question,
    In a Right triangle ADC, Use the (Pythagoras Theorem)
    AC = √DC2 - AD2
    ⇒ AC = √ 152 - 9 2
    ⇒ AC = √ 225 - 81
    ⇒ AC = √ 144
    ⇒ AC = 12 cm
    In a Right triangle BCE, Use the formula
    CB = √ CD2 - BE2
    ⇒ CB = √15 2 - 122
    ⇒ CB = √225 - 144
    ⇒ CB = √ 81
    ⇒ CB = 9 m

    ∴ Width of the street (AC + BC) = AB = 12 + 9 = 21 m.


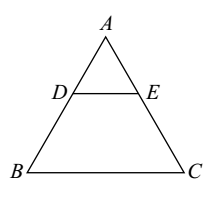
  1. D and E are the points on the sides AB and AC respectively of ΔABC such that AD = 8 cm, BD = 12 cm, AE = 6 cm and EC = 9 cm. Then find BC/ DE.












  1. View Hint View Answer Discuss in Forum

    SinceAD=AE=2
    DBEC3

    ∴ DE || BC (by converse of BPT)
    ∴ ΔADE ∼ ΔABC (AA similarity)

    Correct Option: A

    SinceAD=AE=2
    DBEC3

    ∴ DE || BC (by converse of BPT)
    ∴ ΔADE ∼ ΔABC (AA similarity)
    AD=DE
    ABBC

    8=DE
    ABBC

    2=DE⇒BC=5
    5BCDE2