Plane Geometry
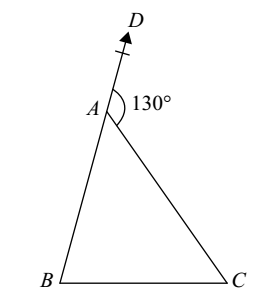
- In the following figure, ∠B : ∠C = 2 : 3, find ∠B + ∠C.
-
View Hint View Answer Discuss in Forum
∠DAC = ∠B + ∠C
(Exterior angle prop. of a Δ ABC)
According to question,
130° = 2A + 3ACorrect Option: D
∠DAC = ∠B + ∠C
(Exterior angle prop. of a Δ ABC)
According to question,
130° = 2A + 3A
5A = 130°
A = 26°
∴ ∠B = 52°; ∠C = 78°
- In a ΔABC, if 2∠A = 3∠B = 6∠C, Then ∠A is equal to:
-
View Hint View Answer Discuss in Forum
Let us assume 2∠A = 3∠B = 6∠C = K
Correct Option: C
Let us assume 2∠A = 3∠B = 6∠C = K
∴ ∠A = k , ∠B = k , ∠C = k , 2 3 6
But ∠A + ∠B + ∠c = 180°∴ k + k + k = 180° 2 3 6
K = 180°Hence, ∠A = 180° = 90° 2
- A, B, C are the three angles of a Δ. If A − B = 15° and B − C = 30°. Then ∠A is equal to :
-
View Hint View Answer Discuss in Forum
Since A, B and C are the angles of a Δ,
∴ A + B + C = 180° .......................................... (1)
According to question,
A – B = 15° ;
⇒ A = B + 15°....................................................(2)
B – C = 30°;
⇒ B = C + 30°;...................................................(3)Correct Option: B
Since A, B and C are the angles of a Δ,
∴ A + B + C = 180° .......................................... (1)
According to question,
A – B = 15° ;
⇒ A = B + 15°....................................................(2)
B – C = 30°;
⇒ B = C + 30°;...................................................(3)
Put the value of B from equation (2) in Equation (1), we will get
∴ A = B + 15°
A = C + 30° + 15°
A = C + 45° ........................................................(4)
From a equation,
∴ A + B + C = 180°
⇒ (C + 45°) + (C + 30°) + C = 180°
⇒ 3C + 45° + 30° = 180°
⇒ 3C = 180° – 75° = 105°
⇒ C = 35° ..........................................................(5)
From equation (4)
A = C + 45°
Put the value of C from equation (5) , we will get
∴ ∠A = 35° + 45° = 80°.
- The sides AB and AC of ΔABC have been produced to D and E respectively. The bisectors of ∠CBD and ∠BCE meet at O. If ∠A = 40°, then ∠BOC is equal to:

-
View Hint View Answer Discuss in Forum
As we know the formula,
∠BOC = 90° - 1 ∠A 2 Correct Option: D
As we know the formula,
∠BOC = 90° - 1 ∠A 2 ∴∠BOC = 90° - 1 (40°) 2
= 90° - 20°
∠BOC = 70°
- Two angles are supplementary and the ratio of the angels is 1:4. what is the value of smaller angle?
-
View Hint View Answer Discuss in Forum
Since the angles are supplementary therefore the sum of their angles will be 180 degree.
Correct Option: A
As we know that the angles are supplementary so sum of angles will be 180 degree.
Let us assume that the ratio factor is r.
According to question,
Angles are supplementary and have a ratio of 1:4.
r + 4r = 180
⇒ 5r = 180
⇒ r = 180/5
⇒ r = 36

