Plane Geometry
- ABCD is a quadrilateral inscribed in a circle with centre O. If ∠COD = 120° and ∠BAC = 30°, then ∠BCD is :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a quadrilateral ABCD inscribed in a circle with centre O
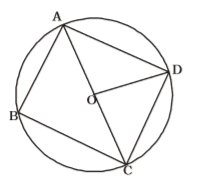
Given , ∠COD = 120°
∠BAC = 30°∠CAD = 1 × ∠COD 2 ∠CAD = 1 × 120° = 60° 2
Correct Option: B
As per the given in question , we draw a figure of a quadrilateral ABCD inscribed in a circle with centre O

Given , ∠COD = 120°
∠BAC = 30°∠CAD = 1 × ∠COD 2 ∠CAD = 1 × 120° = 60° 2
∴ ∠BAD = 90°
∴ ∠BCD = 180° - ∠BAD
∴ ∠BCD = 180° – 90° = 90°
- The radius of two concentric circles are 9 cm and 15 cm. If the chord of the greater circle be a tangent to the smaller circle, then the length of that chord is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,
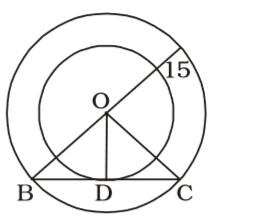
Here , BO = OC = 15 cm and OD = 9 cm.
From ∆ BDO ,
∴ BD = √BO² - OD²Correct Option: A
According to question , we draw a figure of a circle with centre O ,

Here , BO = OC = 15 cm and OD = 9 cm.
From ∆ BDO ,
∴ BD = √BO² - OD²
∴ BD = √15² - 9²
BD = √24 × 6 = 12 cm
∴ BC = 2 × 12 = 24 cm.
- ABC is an isosceles triangle such that AB = AC and ∠B = 35°. AD is the median to the base BC. Then ∠BAD is:
-
View Hint View Answer Discuss in Forum
Firstly , We draw a figure of an isosceles triangle ABC ,

Given that , AB = AC and ∠B = 35°
⇒ ∠ABC = ∠ACB = 35°
Now, ∠ADB = 90°Correct Option: D
Firstly , We draw a figure of an isosceles triangle ABC ,

Given that , AB = AC and ∠B = 35°
⇒ ∠ABC = ∠ACB = 35°
Now, ∠ADB = 90°
In ∆ADB , ∠ BAD + ∠ ABD + ∠ ADB = 180°
⇒ ∠ BAD + 90° + 35° = 180°
∴ ∠BAD = 55°
- The centroid of a triangle is the point where
-
View Hint View Answer Discuss in Forum
As we know the point of intersection of medians of a triangle is called centroid.
Correct Option: A
As we know the centroid of a triangle is the point where the point of intersection of medians of a triangle is called centroid.
- AD is the median of a triangle ABC and O is the centroid such that AO = 10 cm. The length of OD (in cm) is
-
View Hint View Answer Discuss in Forum
According to question ,
D, is the mid-point of side BC. Point O is the centroid that divides AD in the ratio 2 : 1.
we draw a figure triangle ABC whose point O is centroid ,
Correct Option: B
According to question ,
D, is the mid-point of side BC. Point O is the centroid that divides AD in the ratio 2 : 1.
we draw a figure triangle ABC whose point O is centroid ,
AO = 10 cm
∴ OD = 5 cm.

