Plane Geometry
- Suppose ∆ ABC be a right-angled triangle where ∠A = 90° and AD ⊥ BC. If ∆ ABC = 40 cm², ∆ ACD = 10 cm² and AC = 9 cm, then the length of BC is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure right angled triangle CAB
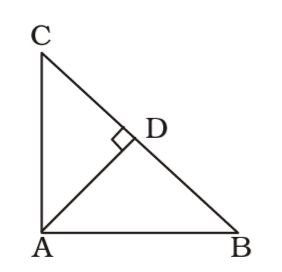
In ∆ACD and ∆ABC,
∠CDA = ∠CAB = 90°
∠C is common.
∴ ∆ACD ~ ∆ABC∴ ∆ACD = AC² ∆ABC BC²
Correct Option: B
According to question , we draw a figure right angled triangle CAB

In ∆ACD and ∆ABC,
∠CDA = ∠CAB = 90°
∠C is common.
∴ ∆ACD ~ ∆ABC∴ ∆ACD = AC² ∆ABC BC² ⇒ 10 = 9² 40 BC²
⇒ BC² = 4 × 9²
∴ BC = 2 × 9 = 18 cm
- In a right angled ∆ ABC, ∠ABC = 90°; BN is perpendicular to AC, AB = 6 cm, AC = 10 cm. Then AN : NC is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure triangle ABC

BC = √10² - 6²
BC = √100 - 36
BC = √64 = 8 cm.Area of ∆ ABC = 1 × BC × AB 2 Area of ∆ ABC = 1 × 8 × 6 = 24Sq. cm. 2 Again, 1 × AC × BN = 24 2 ⇒ 1 × 10 × BN = 24 2 ⇒ BN = 24 5
∴ NC = √BC² - BN²NC = √ 64 - 576 25 NC = 32 cm. 5
Correct Option: B
As per the given in question , we draw a figure triangle ABC

BC = √10² - 6²
BC = √100 - 36
BC = √64 = 8 cm.Area of ∆ ABC = 1 × BC × AB 2 Area of ∆ ABC = 1 × 8 × 6 = 24Sq. cm. 2 Again, 1 × AC × BN = 24 2 ⇒ 1 × 10 × BN = 24 2 ⇒ BN = 24 5
∴ NC = √BC² - BN²NC = √ 64 - 576 25 NC = 32 cm. 5 AN = 10 - 32 = 50 - 32 = 18 5 5 5 ∴ AN : NC = 18 : 32 = 9 : 16 5 5
- ABC is a right angled triangle, right angled at C and p is the length of the perpendicular from C on AB. If a, b and c are the length of the sides BC, CA and AB respectively, then
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of right angle triangle ABC ,

BC = a, AC = b
∴ AB = √AC² + BC²
AB = √b² + a²Area of ∆ ABC = 1 × BC × AC 2 Area of ∆ ABC = 1 ab 2
Again,area of ∆ ABC = 1 × AB × CD 2 area of ∆ ABC = 1 × √a² + b² × p 2 ∴ 1 ab = 1 √a² + b² × p 2 2
⇒ ab = √a² + b² × p
On squaring both sides,
a²b² = (a² + b²) p²⇒ 1 = a² + b² p² a²b² ⇒ 1 = a² + b² p² a²b² a²b²
Correct Option: B
On the basis of question we draw a figure of right angle triangle ABC ,

BC = a, AC = b
∴ AB = √AC² + BC²
AB = √b² + a²Area of ∆ ABC = 1 × BC × AC 2 Area of ∆ ABC = 1 ab 2
Again,area of ∆ ABC = 1 × AB × CD 2 area of ∆ ABC = 1 × √a² + b² × p 2 ∴ 1 ab = 1 √a² + b² × p 2 2
⇒ ab = √a² + b² × p
On squaring both sides,
a²b² = (a² + b²) p²⇒ 1 = a² + b² p² a²b² ⇒ 1 = a² + b² p² a²b² a²b² ⇒ 1 = 1 + 1 = 1 + 1 p² b² a² a² b²
- In ∆ ABC, ∠A = 90° and AD ⊥ BC where D lies on BC. If BC = 8 cm, AC = 6 cm, then ∆ ABC : ∆ ACD =?
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure triangle ABC
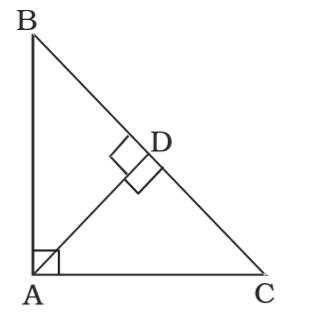
Here , BC = 8 cm, AC = 6 cm,
In ∆ ABC, AD ⊥ BC
⇒ ∆ BAC ~ ∆ ADC
∴ Ratio of area of triangles = ratio of square of their corresponding sides Hence,ar (BAC) = BC² = 64 ar (ADC) AC² 36
Correct Option: C
As per the given in question , we draw a figure triangle ABC

Here , BC = 8 cm, AC = 6 cm,
In ∆ ABC, AD ⊥ BC
⇒ ∆ BAC ~ ∆ ADC
∴ Ratio of area of triangles = ratio of square of their corresponding sides Hence,ar (BAC) = BC² = 64 ar (ADC) AC² 36 Ratio of area of triangles = 16 = 16 : 9 9
- If the median drawn on the base of a triangle is half its base, the triangle will be:
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of triangle ABC ,
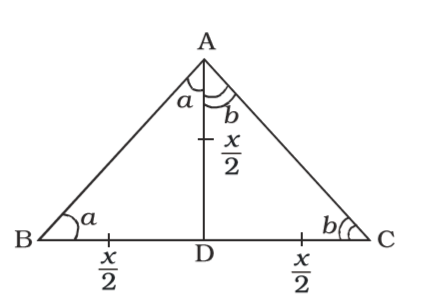
In ∆ ABC,
Let BC = x Since AD is the median,
∴ BD = DC = x/2Also, AD = 1 BC = 1 x or x 2 2 2
Correct Option: A
On the basis of question we draw a figure of triangle ABC ,

In ∆ ABC,
Let BC = x Since AD is the median,
∴ BD = DC = x/2Also, AD = 1 BC = 1 x or x 2 2 2
In ∆ ABD, AD = BD ⇒ ∠BAD = ∠ABD
Similarly
in ∆ ADC,
∠DAC = ∠ACD,
∠A = a + b.
Thus, a + b + a + b = 180°
⇒ a + b = 90°
⇒ ∠A = 90°

