-
ABC is a right angled triangle, right angled at C and p is the length of the perpendicular from C on AB. If a, b and c are the length of the sides BC, CA and AB respectively, then
-
-
1 = 1 - 1 p² b² a² -
1 = 1 + 1 p² a² b² -
1 + 1 = - 1 p² a² b² -
1 = 1 - 1 p² a² b²
-
Correct Option: B
On the basis of question we draw a figure of right angle triangle ABC , 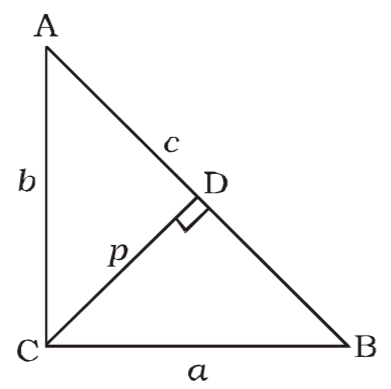
BC = a, AC = b
∴ AB = √AC² + BC²
AB = √b² + a²
| Area of ∆ ABC = | × BC × AC | |
| 2 |
| Area of ∆ ABC = | ab | |
| 2 |
Again,
| area of ∆ ABC = | × AB × CD | |
| 2 |
| area of ∆ ABC = | × √a² + b² × p | |
| 2 |
| ∴ | ab = | √a² + b² × p | ||
| 2 | 2 |
⇒ ab = √a² + b² × p
On squaring both sides,
a²b² = (a² + b²) p²
| ⇒ | = | ||
| p² | a²b² |
| ⇒ | = | + | |||
| p² | a²b² | a²b² |
| ⇒ | = | + | = | + | |||||
| p² | b² | a² | a² | b² |

