Plane Geometry
- If in a triangle ABC, BE and CF are two medians perpendicular to each other and if AB = 19cm and AC = 22 cm then the length of BC is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure triangle ACB in which BE and CF are two medians perpendicular to each other ,

Here , AB = 19cm and AC = 22
FE | | BC
∆ AFE ~ ∆ ABCBC = 1 (AB + AC) 2
Correct Option: C
As per the given in question , we draw a figure triangle ACB in which BE and CF are two medians perpendicular to each other ,

Here , AB = 19cm and AC = 22
FE | | BC
∆ AFE ~ ∆ ABCBC = 1 (AB + AC) 2 BC = 1 (19 + 22) = 20.5 cm. 2
- A point D is taken from the side BC of a right-angled triangle ABC, where AB is hypotenuse. Then
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure right-angled triangle ACB
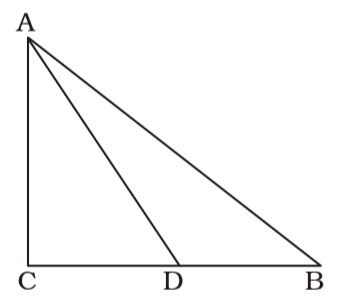
In ∆ABC, AC² + BC² = AB²
In ∆ACD, AD² = AC² + CD²
⇒ AD² – CD² = AC²
∴ AB² + AC² = AC² + BC² + AD² – CD²Correct Option: A
As per the given in question , we draw a figure right-angled triangle ACB

In ∆ABC, AC² + BC² = AB²
In ∆ACD, AD² = AC² + CD²
⇒ AD² – CD² = AC²
∴ AB² + AC² = AC² + BC² + AD² – CD²
⇒ AB² = BC² + AD² – CD²
⇒ AB² + CD² = BC² + AD²
- D and E are two points on the sides AC and BC respectively of ∆ ABC such that DE = 18 cm, CE = 5 cm and ∠DEC = 90°. If tan ∠ABC = 3.6, then AC : CD =
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of triangle ABC ,
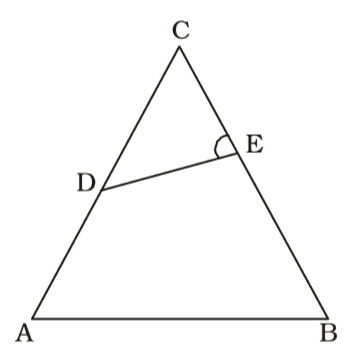
∠DEC = 90°
DE = 18 cm
CE = 5 cm∴ tan C = DE = 18 = 3.6 CE 5
tan ∠ABC = 3.6
⇒ ∠C = ∠B
∴ AC = AB
∠C + ∠D = 90°
⇒ 2 ∠C + 2 ∠D = 180°
∠C + ∠A + ∠B = 180°
⇒ 2C + ∠A = 180°
∴ ∠A = 2 ∠D
Correct Option: C
On the basis of question we draw a figure of triangle ABC ,

∠DEC = 90°
DE = 18 cm
CE = 5 cm∴ tan C = DE = 18 = 3.6 CE 5
tan ∠ABC = 3.6
⇒ ∠C = ∠B
∴ AC = AB
∠C + ∠D = 90°
⇒ 2 ∠C + 2 ∠D = 180°
∠C + ∠A + ∠B = 180°
⇒ 2C + ∠A = 180°
∴ ∠A = 2 ∠D∴ AC = 2CD CB CE ⇒ AC = 2CB or 2BC : CE CD CE
- BL and CM are medians of DABC right-angled at A and BC = 5 cm. If BL = 3√5/2 cm, then the length of CM is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure right-angled triangle BAC

Since BL is the Median AL = LC = x (say). Since CM is the Median, BM = MA = y (say)
AB² + AC² = 25 ...(i)⇒ 
3√5 
² = (2y)² + x² 2 ⇒ 9 × 5 = 4y² + x² 4 ⇒ 4y² = 45 - x² ...(ii) 4
In ∆ ABC, BC² = AB² + AC²
⇒ 25 = (2y)² + (2x)²
25 = 4y² + 4x²⇒ 25 = 45 - x² + 4y² 4 3x² = 55 ⇒ x² = 55 4 12 Put in (ii) ⇒ 4y² = 45 - 55 4 12 ⇒ 4y² = 135 - 55 12 ⇒ 4y² = 80 ⇒ y² = 80 = 5 12 12 × 4 3
Now , CM = √y² + 4x²CM = √ 5 + 4 
55 
3 12
Correct Option: A
According to question , we draw a figure right-angled triangle BAC

Since BL is the Median AL = LC = x (say). Since CM is the Median, BM = MA = y (say)
AB² + AC² = 25 ...(i)⇒ 
3√5 
² = (2y)² + x² 2 ⇒ 9 × 5 = 4y² + x² 4 ⇒ 4y² = 45 - x² ...(ii) 4
In ∆ ABC, BC² = AB² + AC²
⇒ 25 = (2y)² + (2x)²
25 = 4y² + 4x²⇒ 25 = 45 - x² + 4y² 4 3x² = 55 ⇒ x² = 55 4 12 Put in (ii) ⇒ 4y² = 45 - 55 4 12 ⇒ 4y² = 135 - 55 12 ⇒ 4y² = 80 ⇒ y² = 80 = 5 12 12 × 4 3
Now , CM = √y² + 4x²CM = √ 5 + 4 
55 
3 12 CM = √ 5 + 55 3 3 CM = √ 60 3
CM = √20 = 2 √5cm.
- The ortho center of a right angled triangle lies
-
View Hint View Answer Discuss in Forum
According to question ,
When orthocenter lies at right angular vertex, then the triangle is right angled.Correct Option: B
According to question ,
When orthocenter lies at right angular vertex, then the triangle is right angled. Hence , option B is correct answer .

