Plane Geometry
- The ratio of the angles ∠A and ∠B of a non-square rhombus ABCD is 4 : 5, then the value of ∠C is :
-
View Hint View Answer Discuss in Forum
Given , The ratio of the angles ∠A and ∠B of a non-square rhombus ABCD = 4 : 5
Let 4y and 5y are angles .
⇒ 4y + 5y = 180°
⇒ 9y = 180°Correct Option: C
Given , The ratio of the angles ∠A and ∠B of a non-square rhombus ABCD = 4 : 5
Let 4y and 5y are angles .
⇒ 4y + 5y = 180°
⇒ 9y = 180°
⇒ y = 20°
∴ ∠C = 4y = 80°
- In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of quadrilateral ABCD

OB² + OC² = BC²
OC² + OD² = CD²
OD² + OA² = AD²
OA² + OB² = AB²
Pythagoras theorem
∴ 2 (OB² + OA² + OD² + OC²) = AB² + BC² + CD² + DA²
Correct Option: B
On the basis of question we draw a figure of quadrilateral ABCD

OB² + OC² = BC²
OC² + OD² = CD²
OD² + OA² = AD²
OA² + OB² = AB²
Pythagoras theorem
∴ 2 (OB² + OA² + OD² + OC²) = AB² + BC² + CD² + DA²
⇒ 2(AB² + CD²) = AB² + BC² + CD² + DA²
⇒ AB² + CD² = BC² + DA²
- ABCD is a rhombus. A straight line through C cuts AD produced at P and AB produced at Q. If DP = ( 1/2 )AB, then the ratio of the length of BQ and AB is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of rhombus ABCD and straight line through C cuts AD produced at P and AB produced at Q ,
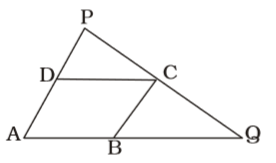
AB = BC = CD = DA
[ABCD is a rhombus]DP = 1 AB = 1 BC = 1 CD = 1 DA 2 2 2 2
In ∆s APQ and BCQ,
∴ ∆ APQ and ∆ BCQ are similar.∴ AB + BQ = AD + DP BQ BC ⇒ AB + 1 = ( 3/2 )BC = 3 BQ BC 2 ⇒ AB = 3 - 1 = 1 BQ 2 2
Correct Option: A
According to question , we draw a figure of rhombus ABCD and straight line through C cuts AD produced at P and AB produced at Q ,

AB = BC = CD = DA
[ABCD is a rhombus]DP = 1 AB = 1 BC = 1 CD = 1 DA 2 2 2 2
In ∆s APQ and BCQ,
∴ ∆ APQ and ∆ BCQ are similar.∴ AB + BQ = AD + DP BQ BC ⇒ AB + 1 = ( 3/2 )BC = 3 BQ BC 2 ⇒ AB = 3 - 1 = 1 BQ 2 2 ⇒ BQ = 2 AB 1
⇒ BQ : AB = 2 : 1
- ABCD is a cyclic quadrilateral of which AB is the diameter. Diagonals AC and BD intersect at E. If ∠DBC = 35°, then ∠AED measures
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of cyclic quadrilateral ABCD and AB is a diameter ,

The angle in a semi-circle is right angle.
∴ ∠ADB = ∠ACB = 90°
Given that , ∠DBC = 35°Correct Option: C
According to question , we draw a figure of cyclic quadrilateral ABCD and AB is a diameter ,

The angle in a semi-circle is right angle.
∴ ∠ADB = ∠ACB = 90°
Given that , ∠DBC = 35°
∴ ∠CEB = 90° – 35° = 55°
∴ ∠CEB = ∠AED = 55°
(Opposite angles)
- In a cyclic quadrilateral ABCD, the side AB is extended to a point X. If ∠XBC = 82° and ∠ADB = 47°, then the value of ∠BDC is :
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of cyclic quadrilateral ABCD in which the side AB is extended to a point X ,

We know that the sum of opposite angles of a cyclic quadrilateral is 180°.
Given , ∠CBX = 82°
∴ ∠ABC = 180° – 82° = 98°
∴ ∠ADC + ∠ABC = 180°Correct Option: B
On the basis of question we draw a figure of cyclic quadrilateral ABCD in which the side AB is extended to a point X ,

We know that the sum of opposite angles of a cyclic quadrilateral is 180°.
Given , ∠CBX = 82°
∴ ∠ABC = 180° – 82° = 98°
∴ ∠ADC + ∠ABC = 180°
⇒ ∠ADC = 180° – 98° = 82°
∠ADB = 47° .
∴ ∠BDC = 82° – 47° = 35°

