Plane Geometry
- Two chords AB and CD of a circle with centre O intersect at P. If ∠APC = 40°. Then the value of ∠AOC + ∠BOD is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,
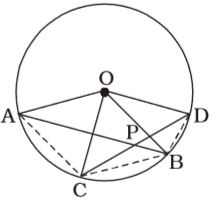
Given , ∠APC = 40°.
Arc AC subtends ∠AOC at the centre and ∠ABC at the circumference.
Similarly, ∠BOD = 2∠BCDCorrect Option: C
According to question , we draw a figure of a circle with centre O ,

Given , ∠APC = 40°.
Arc AC subtends ∠AOC at the centre and ∠ABC at the circumference.
Similarly, ∠BOD = 2∠BCD
∴ ∠AOC + ∠BOD = 2 (∠ABC + ∠BCD)
∠AOC + ∠BOD = 2 ∠APC = 2 × 40° = 80°
- In a circle with centre O, AB is a diameter and CD is a chord which is equal to the radius OC. AC and BD are extended in such a way that they intersect each other at a point P, exterior to the circle. The measure of ∠APB is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a circle with centre O,
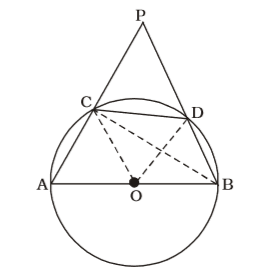
In ∆ OCD,
OC = OD = CD = radius
∴ ∆ OCD is an equilateral triangle.
∴ ∠COD = 60°∠CBD = 1 ∠COD = 30° 2
∠ACB is an angle of semi-circle.
∴ ∠ACB = 90°
Correct Option: C
As per the given in question , we draw a figure of a circle with centre O,

In ∆ OCD,
OC = OD = CD = radius
∴ ∆ OCD is an equilateral triangle.
∴ ∠COD = 60°∠CBD = 1 ∠COD = 30° 2
∠ACB is an angle of semi-circle.
∴ ∠ACB = 90°
∴ ∠BCP = 180° – ∠ACB
∠BCP = 180° – 90° = 90°
In ∆ BCP, ∠BCP = 90°,∠CBP = ∠CBD = 30°
∴ ∠BCP + ∠CBP + ∠CPB = 180°
⇒ 90° + 30° + ∠CPB = 180°
⇒ ∠CPB = 60° = ∠APB
- In a circle, a diameter AB and a chord PQ (which is not a diameter) intersect each other at X perpendicularly. If AX : BX = 3 : 2 and the radius of the circle is 5 cm, then the length of chord PQ is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,
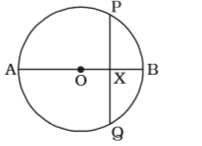
Here , AX : BX = 3 : 2AX = 3 BX 2 ∴ AX = 3 × 10 = 6 cm. 5 ∴ BX = 2 × 10 = 4 cm. 5
Correct Option: C
According to question , we draw a figure of a circle with centre O ,

Here , AX : BX = 3 : 2AX = 3 BX 2 ∴ AX = 3 × 10 = 6 cm. 5 ∴ BX = 2 × 10 = 4 cm. 5
∴ AX × XB = PX²
⇒ PX² = 6 × 4
⇒ PX = √6 × 4 = 2 √6
∴ PQ = 2PX = 4√6 cm.
- Two circles touch each other internally. The radius of the larger circle is 6 cm and the distance between the centre is 2 cm, then the radius (in cms) of the other circle is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of two circles touch each other internally ,
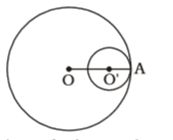
The radius of the larger circle ( r1 ) = 6 cm
and the distance between the centre ( OO' ) = 2 cmCorrect Option: C
As per the given in question , we draw a figure of two circles touch each other internally ,

The radius of the larger circle ( r1 ) = 6 cm
and the distance between the centre ( OO' ) = 2 cm
As we know that , OO' = r1 + r2
Radius of other circle = 6 – 2 = 4 cm.
- Two chords AB and PQ of a circle intersect at D inside a circle. If AD = 4 cm., DB = 6 cm., QD = 3 cm., the length of PQ is equal to
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,
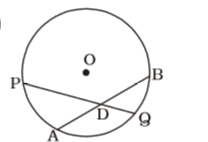
Here , AD = 4 cm., DB = 6 cm., QD = 3 cm
As we know that , AD × DB = PD × DQ
⇒ 4 × 6 = PD × 3Correct Option: A
According to question , we draw a figure of a circle with centre O ,

Here , AD = 4 cm., DB = 6 cm., QD = 3 cm
As we know that , AD × DB = PD × DQ
⇒ 4 × 6 = PD × 3⇒ PD = 4 × 6 = 8 cm. 3
∴ PQ = PD + DQ = (8 + 3) cm. = 11 cm.

