Plane Geometry
- If the measures of the sides of triangle are (x2 – 1), (x2 + 1) and 2x cm, then the triangle would be
-
View Hint View Answer Discuss in Forum
Let a = (x2 – 1), b = (x2 + 1) and c = 2x cm,
Now c² + a² = (2x)² + (x² – 1)²
c² + a² = 4x² + x² – 2x² + 1
c² + a² = x² + 2x² + 1
c² + a² = (x² + 1)² = b²Correct Option: D
Let a = (x2 – 1), b = (x2 + 1) and c = 2x cm,
Now c² + a² = (2x)² + (x² – 1)²
c² + a² = 4x² + x² – 2x² + 1
c² + a² = x² + 2x² + 1
c² + a² = (x² + 1)² = b²
From above clear that it is a right angled triangle .
- If each angle of a triangle is less than the sum of the other two, then the triangle is
-
View Hint View Answer Discuss in Forum
According to question ,
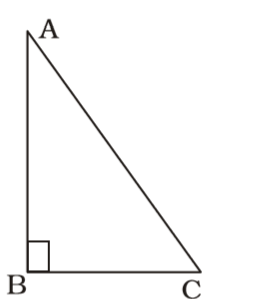
In right angled ∆ ABC,
B² = A² + C²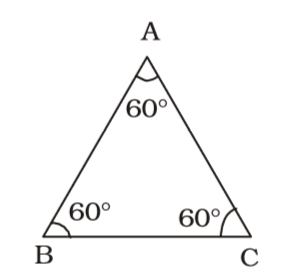
In an equilateral triangle ABC,∠B = ∠A + ∠C 2 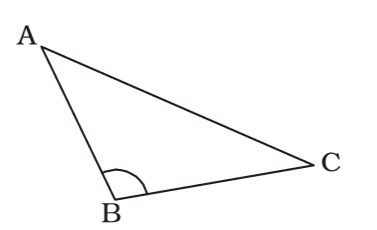
In obtuse angled triangle,
∠B > ∠A + ∠C
In acute angled triangle ABC,
∠A < ∠B + ∠C
∠B < ∠A + ∠CCorrect Option: C
According to question ,

In right angled ∆ ABC,
B² = A² + C²
In an equilateral triangle ABC,∠B = ∠A + ∠C 2 
In obtuse angled triangle,
∠B > ∠A + ∠C
In acute angled triangle ABC,
∠A < ∠B + ∠C
∠B < ∠A + ∠C
Hence , correct answer is option C .
- ABC is a right-angled triangle with AB = 6 cm and BC = 8 cm. A circle with centre O has been inscribed inside ∆ABC. The radius of the circle is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure right-angled triangle ABC in which inscribed inside a circle with centre O ,
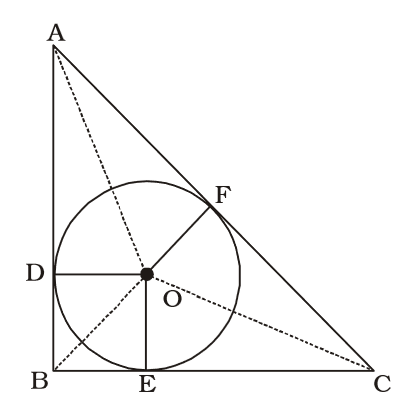
AC = √AB² + BC²
AC = √6² + 8²
AC = √36 + 64
AC = √100 = 10 cm
OD = OE = OF = radii = r cm
∴ Area of [∆ AOB + ∆ BOC + ∆ AOC] = ∆ABC⇒ 1 × 6 × r + 1 × 8 × r + 1 × 10 × r = 1 × 8 × 6 2 2 2 2
Correct Option: B
As per the given in question , we draw a figure right-angled triangle ABC in which inscribed inside a circle with centre O ,

AC = √AB² + BC²
AC = √6² + 8²
AC = √36 + 64
AC = √100 = 10 cm
OD = OE = OF = radii = r cm
∴ Area of [∆ AOB + ∆ BOC + ∆ AOC] = ∆ABC⇒ 1 × 6 × r + 1 × 8 × r + 1 × 10 × r = 1 × 8 × 6 2 2 2 2
⇒ 3r + 4r + 5r = 24
⇒ 12r = 24⇒ r = 24 = 12 cm. 2
- If the sides of a right angled triangle are three consecutive integers, then the length of the smallest side is
-
View Hint View Answer Discuss in Forum
In right angled triangle PQR,

From right angle triangle , PQ² + QR² = PR²
According to question ,
Here, 3² + 4² = 5²Correct Option: A
In right angled triangle PQR,

From right angle triangle , PQ² + QR² = PR²
According to question ,
Here, 3² + 4² = 5²
∴ The smallest side = 3 units
- The angle in a semi-circle is
-
View Hint View Answer Discuss in Forum
Angle in a semi-circle is a right angle.
Correct Option: D
As we know that Angle in a semi-circle is a right angle.

