As per the given in question , we draw a figure of circle with centre O and PT is a tangent

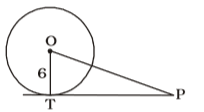
Given that , OT = 6 cm. , TP = 8 cm.
∠OTP = 90°
In ∆ OPT,

Correct Option: A

As per the given in question , we draw a figure of circle with centre O and PT is a tangent

Given that , OT = 6 cm. , TP = 8 cm.
∠OTP = 90°
In ∆ OPT,
OP = √OT² + TP² = √6² + 8²
OP = √36 + 64 = 100 = 10 cm.

On the basis of question we draw a figure of a circle with centre O

Tangent ⇒ CAD
OA ⊥ CD
⇒ OAD = 90° ∠BAD = θ = ∠OBA

Correct Option: B

On the basis of question we draw a figure of a circle with centre O

Tangent ⇒ CAD
OA ⊥ CD
⇒ OAD = 90° ∠BAD = θ = ∠OBA
From ∆AOB ,
∴ ∠OAB = 90° – θ = ∠OBA

As per the given in question , we draw a figure of circle with centre O and P is an external point of it at a distance of 13 cm from O

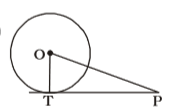
Givne that , OT = 5 cm.
OP = 13 cm.
From ∆PTO ,
∴ PT = √OP² - OT²

Correct Option: C

As per the given in question , we draw a figure of circle with centre O and P is an external point of it at a distance of 13 cm from O

Givne that , OT = 5 cm.
OP = 13 cm.
From ∆PTO ,
∴ PT = √OP² - OT²
PT = √13² - 5²
PT = √169 - 25 = √144 = 12 cm.

As per the given in question , we draw a figure of circle in which PQ and PR be the two tangents

PQ = PR (Tangents from the same exterior point)
Given , ∠QPR = 120°

Correct Option: C

As per the given in question , we draw a figure of circle in which PQ and PR be the two tangents

PQ = PR (Tangents from the same exterior point)
Given , ∠QPR = 120°

According to question , we draw a figure of two circles and T is a point on the common tangents at P

We can say that tangents drawn from an external point to a circle are equal.

Correct Option: B

According to question , we draw a figure of two circles and T is a point on the common tangents at P

We can say that tangents drawn from an external point to a circle are equal.
∴ TA = TP; TP = TB
∴ TA = TB