Plane Geometry
- In a circle of radius 21 cm, an arc subtends an angle of 72° at the centre. The length of the arc is
-
View Hint View Answer Discuss in Forum
Here , Rradius ( r ) = 21 cm
θ = 72° = 72 × π radians 180 θ = 2π radians 5
As we know that ,∴ θ = l r
l → length of arc⇒ l = θ.r = 2π × 21 5
Correct Option: B
Here , Rradius ( r ) = 21 cm
θ = 72° = 72 × π radians 180 θ = 2π radians 5
As we know that ,∴ θ = l r
l → length of arc⇒ l = θ.r = 2π × 21 5 l = 2 × 22 × 21 5 7 l = 132 = 26.4 cm. 5
- The distance between two parallel chords of length 8 cm each in a circle of diameter 10 cm is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure circle
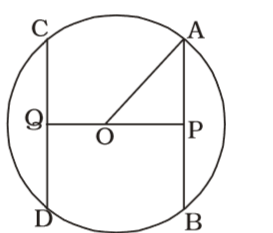
Given , Diameter = 10 cm
AB = CD
OP = OQ
From ∆ OAP,
OP = √OA² - AP²
OP = √5² - 4²
OP = √25 - 16Correct Option: A
As per the given in question , we draw a figure circle

Given , Diameter = 10 cm
AB = CD
OP = OQ
From ∆ OAP,
OP = √OA² - AP²
OP = √5² - 4²
OP = √25 - 16
OP = √9 = 3 cm.
∴ QP = 2 × OP = 6 cm.
- The length of two chords AB and AC of a circle are 8 cm and 6 cm and ∠BAC = 90°, then the radius of circle is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with two chords AB and AC ,
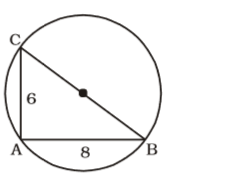
Here , AB = 8 cm and AC = 6 cm
∠ BAC = 90°
As, BC is the diameter of the circle.
∴ BC = √AB² + AC²
BC = √8² + 6²
BC = √64 + 36Correct Option: E
According to question , we draw a figure of a circle with two chords AB and AC ,

Here , AB = 8 cm and AC = 6 cm
∠ BAC = 90°
As, BC is the diameter of the circle.
∴ BC = √AB² + AC²
BC = √8² + 6²
BC = √64 + 36
BC = √100 = 10 cm
∴ Radius of the circle = 5 cm
- The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends in the major segment of the circle is equal to
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure circle
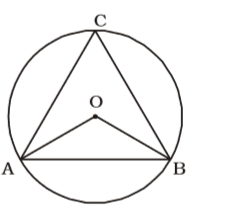
AO = OB = AB
⇒ ∠AOB = 60°Correct Option: A
As per the given in question , we draw a figure circle

AO = OB = AB
⇒ ∠AOB = 60°
[∵ ∆ AOB is equilateral]
∴ ∠ ACB = 30°
- The length of the chord of a circle is 8 cm and perpendicular distance between centre and the chord is 3 cm. Then the radius of the circle is equal to :
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of circle with O centre ,

AC = CB = 4 cm
OC = 3 cm
∴ OA = √OC² + CA²
OA = √3² + 4²Correct Option: B
On the basis of question we draw a figure of circle with O centre ,

AC = CB = 4 cm
OC = 3 cm
∴ OA = √OC² + CA²
OA = √3² + 4²
OA = √9 + 16
OA = √25 = 5 cm

