Plane Geometry
- In the given diagram, an incircle DEF is circumscribed by the right angled triangle in which AF = 6 cm and EC = 15 cm. Then find the difference between CD and BD.
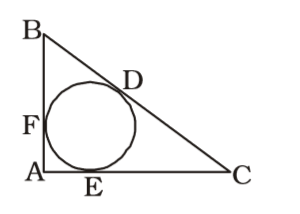
-
View Hint View Answer Discuss in Forum
As per the given figure in question ,
OE = OF (In–radius)
BF = BD (tangents from external point B)
and EC = DC = 15 cm.
Let BF = y cm. AB = (6 + y) cm.
AC = 6 + 15 = 21 cm.
From ∆ABC ,
BC² = AB² + AC²
⇒ (y + 15)² = (6 + y)² + (21)²
(∵ BC = BD + CD)
⇒ y² + 30y + 225 = 36 + y² + 12y + 441Correct Option: A
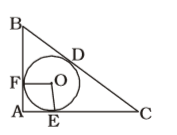
As per the given figure in question ,

OE = OF (In–radius)
BF = BD (tangents from external point B)
and EC = DC = 15 cm.
Let BF = y cm. AB = (6 + y) cm.
AC = 6 + 15 = 21 cm.
From ∆ABC ,
BC² = AB² + AC²
⇒ (y + 15)² = (6 + y)² + (21)²
(∵ BC = BD + CD)
⇒ y² + 30y + 225 = 36 + y² + 12y + 441
⇒ 30y – 12y = 441 + 36 – 225
⇒ 18y = 252⇒ y = 252 = 14 ⇒ BD = 14 cm. 18
∴ Required difference = CD – BD = 15 – 14 = 1 cm.
- O is the circumcentre of the isosceles ∆ABC. Given that AB = AC = 17 cm. and BC = 6 cm. The radius of the circle is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of isosceles triangle ABC in which O is the circumcentre
AB = AC = 5 cm. (We have assumed to reach answer)
AD ⊥ BC
BD = DC = 3 cm.
In ∆ ADB ,
AD = √AB² - BD²
AD = √5² - 3²
AD = √25 - 9 = √16 = 4 cm.
Let, OA = OC = r cm.
OD = (4 – r) cm.
In ∆ OCD,Correct Option: D
According to question , we draw a figure of isosceles triangle ABC in which O is the circumcentre

AB = AC = 5 cm. (We have assumed to reach answer)
AD ⊥ BC
BD = DC = 3 cm.
In ∆ ADB ,
AD = √AB² - BD²
AD = √5² - 3²
AD = √25 - 9 = √16 = 4 cm.
Let, OA = OC = r cm.
OD = (4 – r) cm.
In ∆ OCD,
OC² = OD² + DC²
⇒ r² = (4 – r)² + 3²
⇒ r² = 16 + r² – 8r + 9
⇒ 8r = 25
⇒ r = 25 ÷ 8 = 3.125
- A chord of a circle is equal to its radius. The angle subtended by this chord at a point on the circumference is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle whose a chord is equal to its radius

OA = OB = AB
∴ ∆ OAB is an equilateral triangle.
∴ ∠AOB = 60°Correct Option: C
According to question , we draw a figure of a circle whose a chord is equal to its radius

OA = OB = AB
∴ ∆ OAB is an equilateral triangle.
∴ ∠AOB = 60°∴ ∠ACB = 60° = 30° 2
Angle subtended at the centre by an arc is twice to that at the circumference.
- If O is the circumcentre of a triangle ABC lying inside the triangle, then ∠OBC + ∠BAC is equal to
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a triangle ABC and O is the circumcentre
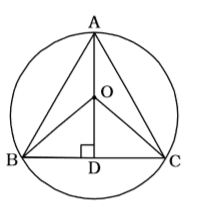
In ∆ OBC ∵ OB = OC
∴ ∠ OBC = ∠OCB
∴ ∠ BOC = 180° – 2 ∠OBC
In ∆ OBD,
∠OBD = ∠ OBC = 90° – ∠BOD
Angle subtended by an arc at the centre is twice to that subtended at the circumference.∴ ∠BAC = 1 ∠OBC 2
Correct Option: A
As per the given in question , we draw a figure of a triangle ABC and O is the circumcentre

In ∆ OBC ∵ OB = OC
∴ ∠ OBC = ∠OCB
∴ ∠ BOC = 180° – 2 ∠OBC
In ∆ OBD,
∠OBD = ∠ OBC = 90° – ∠BOD
Angle subtended by an arc at the centre is twice to that subtended at the circumference.∴ ∠BAC = 1 ∠OBC 2 ∠BAC = 1 (180° - 2∠OBC 2
∠BAC = 90° - ∠OBC
∴ ∠BAC + ∠OBC = 90°
- O is the circumcentre of the triangle ABC and °BAC = 85°, °BCA = 75°, then the value of °OAC is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a triangle ABC whose the circumcentre is O ,

Here , ∠BAC = 85°
∠BCA = 75°
∠ABC = 180° – 85° – 75° = 20°
We can say that angle subtended by an arc at the centre is twice to that subtended at any point on the circumference.
∴ 2∠ABC = ∠AOC
∴ ∠OAC = 40°
In ∆ OAC,
OA = OC = radiiCorrect Option: D
On the basis of question we draw a figure of a triangle ABC whose the circumcentre is O ,

Here , ∠BAC = 85°
∠BCA = 75°
∠ABC = 180° – 85° – 75° = 20°
We can say that angle subtended by an arc at the centre is twice to that subtended at any point on the circumference.
∴ 2∠ABC = ∠AOC
∴ ∠OAC = 40°
In ∆ OAC,
OA = OC = radii
∴ ∠OAC = ∠OCA
∴ 2∠OAC = 180° – 40° = 140°⇒ ∠OAC = 140° = 70° 2

