Plane Geometry
- In ∆ ABC, ∠B is right angle, D is the mid–point of the side AC. If AB = 6 cm, BC = 8 cm, then the length of BD is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of right angle triangle ABC in which D is the mid–point of the side AC ,

In ∆ ABC,
AC = √AB² + BC²
AC = √6² + 8²
AC = √36 + 64
AC = √100 = 10 cm.Correct Option: B
On the basis of question we draw a figure of right angle triangle ABC in which D is the mid–point of the side AC ,

In ∆ ABC,
AC = √AB² + BC²
AC = √6² + 8²
AC = √36 + 64
AC = √100 = 10 cm.
A circle will pass through the points A, B, and C such that AC is diameter as ∠B = 90°.
∴ AD = BD = DC = 5 cm.
- In a right angled triangle if hypotenuse is 20 cm and ratio of other two sides is 4 : 3, the lengths of the sides are
-
View Hint View Answer Discuss in Forum
Let the other sides of right angled triangle be 4y and 3y cm.
∴ (Perpendicular)² + (Base)² = (Hypotenuse)²
⇒ (4y)² + (3y)² = (20)²
⇒ 16y² + 9y² = 400
⇒ 25y² = 400⇒ y² = 400 = 16 25
Correct Option: D
Let the other sides of right angled triangle be 4y and 3y cm.
∴ (Perpendicular)² + (Base)² = (Hypotenuse)²
⇒ (4y)² + (3y)² = (20)²
⇒ 16y² + 9y² = 400
⇒ 25y² = 400⇒ y² = 400 = 16 25
∴ y = √16 = 4
∴ Other sides of triangle = 4y = 4 × 4 = 16 cm. and 3y = 3 × 4 = 12 cm.
- XYZ is a right angled triangle and ∠Y = 90°. If XY = 2.5 cm and YZ = 6 cm then the circumradius of ∆ XYZ is :
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure triangle XYZ
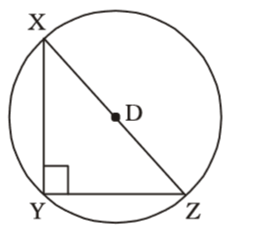
XY = 2.5 cm
YZ = 6 cm
∴ XZ = √XY² + YZ²
XZ = √(2.5)² + (6)²
XZ = √6.25 + 36
XZ = √42.25 = 6.5 cmCorrect Option: B
According to question , we draw a figure triangle XYZ

XY = 2.5 cm
YZ = 6 cm
∴ XZ = √XY² + YZ²
XZ = √(2.5)² + (6)²
XZ = √6.25 + 36
XZ = √42.25 = 6.5 cm
The angle of semi-circle is right angle.
∴ XZ = Diameter of circle
∴ Circum-radius = 65 ÷ 2 = 3.25 cm
- In a right angled triangle ∆ DEF, if the length of the hypotenuse EF is 12 cm, then the length of the median DX is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of right-angled triangle FDE
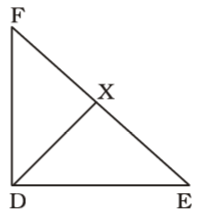
ED The median splits the right triangle into two isosceles triangles and the median is half the length of the hypotenuse.Correct Option: C
As per the given in question , we draw a figure of right-angled triangle FDE

ED The median splits the right triangle into two isosceles triangles and the median is half the length of the hypotenuse.
∴ EF = 12 cm.
⇒ DX = XE = XF = 6 cm.
- In ∆PQR, S and T are points on sides PR and PQ respectively such that ∠PQR = ∠PST. If PT = 5 cm, PS = 3 cm and TQ = 3 cm, then length of SR is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw figures of two similar triangles PQR and PST
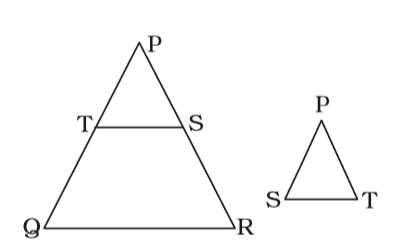
Here , PT = 5 cm, PS = 3 cm and TQ = 3 cm
∠PQR = ∠PST
∠P = ∠P
∴ ∆PST and ∆PQR are similar,∴ PQ = PR PS PT ⇒ 8 = PR 3 5 ⇒ PR = 8 × 5 = 40 3 3 ∴ SR = PR - PS = 40 - 3 3
Correct Option: C
As per the given in question , we draw figures of two similar triangles PQR and PST

Here , PT = 5 cm, PS = 3 cm and TQ = 3 cm
∠PQR = ∠PST
∠P = ∠P
∴ ∆PST and ∆PQR are similar,∴ PQ = PR PS PT ⇒ 8 = PR 3 5 ⇒ PR = 8 × 5 = 40 3 3 ∴ SR = PR - PS = 40 - 3 3 SR = PR = PS = 40 - 9 = 31 cm. 3 3

