Plane Geometry
- ∆ ABC is an isosceles triangle in which AB = AC. Side BA is extended to D such that AB = AD. What will be the value of∠BCD ?
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure an isosceles triangle ABC in which AB = AC and side BA is extended to D such that AB = AD

In ∆ ABC,
AB = AC
⇒ ∠ACB = ∠ABC ..... (i)
Now, AB = AD
∴ AD = AC
In ∆ ADC,
AD = AC
⇒ ∠ACD = ∠ADC ....(ii)
By equations (i) + (ii),
∠ACB + ∠ACD = ∠ABC + ∠ADC
⇒∠BCD = ∠ABC + ∠BDCCorrect Option: A
As per the given in question , we draw a figure an isosceles triangle ABC in which AB = AC and side BA is extended to D such that AB = AD

In ∆ ABC,
AB = AC
⇒ ∠ACB = ∠ABC ..... (i)
Now, AB = AD
∴ AD = AC
In ∆ ADC,
AD = AC
⇒ ∠ACD = ∠ADC ....(ii)
By equations (i) + (ii),
∠ACB + ∠ACD = ∠ABC + ∠ADC
⇒∠BCD = ∠ABC + ∠BDC
⇒∠BCD + ∠BCD = ∠ABC + ∠BDC + ∠BCD
⇒ 2 ∠BCD = 180°
⇒∠BCD = 90°
- In any triangle ABC the internal bisector of ∠ABC and the external bisector of other base angle meet at point E. Then ∠BEC = ?
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a triangle ABC in which the internal bisector of ∠ABC and the external bisector of other base angle meet at point E

As we know that , Exterior angle = Sum of two alternate angles
Exterior ∠ACD = ∠A + ∠B⇒ 1 ∠ACD = 1 ∠A + 1 ∠B 2 2 2 ⇒∠ 2 = ∠ 1 + 1 ∠A.........(i) 2
In ∆ BCE,
∠ ECD = ∠1 + ∠E
⇒∠ 2 = ∠ 1 + ∠ E .........(ii)
From equations (i) and (ii),
Correct Option: C
According to question , we draw a figure of a triangle ABC in which the internal bisector of ∠ABC and the external bisector of other base angle meet at point E

As we know that , Exterior angle = Sum of two alternate angles
Exterior ∠ACD = ∠A + ∠B⇒ 1 ∠ACD = 1 ∠A + 1 ∠B 2 2 2 ⇒∠ 2 = ∠ 1 + 1 ∠A.........(i) 2
In ∆ BCE,
∠ ECD = ∠1 + ∠E
⇒∠ 2 = ∠ 1 + ∠ E .........(ii)
From equations (i) and (ii),∠1 + 1 ∠A = ∠1 + ∠E 2 ⇒ 1 ∠A = ∠E 2 ⇒ ∠E = 1 ∠A 2
- In any triangle PQR, PS is the internal bisector of∠QPR and PT ⊥ QR then ∠TPS = ?
-
View Hint View Answer Discuss in Forum
On the basis of given question , we draw a figure of triangle PQR in which PS is the internal bisector of∠QPR and PT ⊥ QR
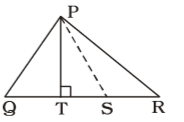
PS, is bisector of ∠QPR.
∴ ∠QPS = ∠SPR .....(i)
In ∆
PQT, ∠PQT + ∠PTQ + ∠QPT = 180°
⇒ ∠PQT + 90° + ∠QPT = 180°
⇒ ∠PQT + ∠QPT = 90°
⇒ ∠PQT = 90° – ∠QPT
⇒ ∠Q = 90° – ∠QPT .....(ii)
In ∆ PTR,
∠PRT + ∠TPR + ∠PTR = 180°
⇒ ∠PRT + ∠TPR + 90° = 180°
⇒ ∠PRT + ∠TPR = 90°
⇒ ∠PRT = 90° – ∠TPR ....(iii)
By equation (ii) – (iii),
∠Q – ∠R = (90° – ∠QPT) – (90° – ∠TPR)
⇒ ∠Q – ∠R = ∠TPR – ∠QPTCorrect Option: C
On the basis of given question , we draw a figure of triangle PQR in which PS is the internal bisector of∠QPR and PT ⊥ QR

PS, is bisector of ∠QPR.
∴ ∠QPS = ∠SPR .....(i)
In ∆
PQT, ∠PQT + ∠PTQ + ∠QPT = 180°
⇒ ∠PQT + 90° + ∠QPT = 180°
⇒ ∠PQT + ∠QPT = 90°
⇒ ∠PQT = 90° – ∠QPT
⇒ ∠Q = 90° – ∠QPT .....(ii)
In ∆ PTR,
∠PRT + ∠TPR + ∠PTR = 180°
⇒ ∠PRT + ∠TPR + 90° = 180°
⇒ ∠PRT + ∠TPR = 90°
⇒ ∠PRT = 90° – ∠TPR ....(iii)
By equation (ii) – (iii),
∠Q – ∠R = (90° – ∠QPT) – (90° – ∠TPR)
⇒ ∠Q – ∠R = ∠TPR – ∠QPT
⇒ ∠Q – ∠R = (∠TPS + ∠SPR) – (∠QPS – ∠TPS)
⇒ ∠Q – ∠R = 2 ∠TPS⇒ ∠TPS = 1 (∠Q - ∠R) 2
- If the internal bisectors of angles ∠ABC and ∠ACB of ∆ABC intersect at point O, then ∠BOC = ?
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure a ∆ ABC and the internal bisectors of angles ∠ABC and ∠ACB intersect at point O
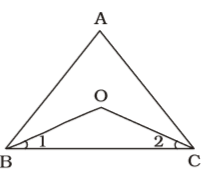
In ∆ BOC,
We know that sum of all three angles is 180°
∠1 + ∠2 + ∠BOC = 180° ...(i)
In ∆ ABC,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 2 ∠1 + 2 ∠2 = 180°⇒ ∠A + ∠1 + ∠2 = 90° 2 ⇒ ∠1 + ∠2 = 90° - ∠A 2
From equation (i) ,
Correct Option: B
As per the given in question , we draw a figure a ∆ ABC and the internal bisectors of angles ∠ABC and ∠ACB intersect at point O

In ∆ BOC,
We know that sum of all three angles is 180°
∠1 + ∠2 + ∠BOC = 180° ...(i)
In ∆ ABC,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 2 ∠1 + 2 ∠2 = 180°⇒ ∠A + ∠1 + ∠2 = 90° 2 ⇒ ∠1 + ∠2 = 90° - ∠A 2
From equation (i) ,90° – ∠A + ∠BOC = 180° 2 ⇒ ∠BOC = 180° – 90° + ∠A = 90° + ∠A 2 2
- The angles of a triangle are in the ratio of 1 : 2 : 3. What will be the radian measure of the largest angle of the triangle ?
-
View Hint View Answer Discuss in Forum
As we know that Sum of all angles of a traingle = 180°
The ratio of angles of a triangle = 1 : 2 : 3.
∴ Sum of ratios = 1 + 2 + 3 = 6∴ Largest angle = 3 × 180° = 90° 6
∵ 180° = π radian
Correct Option: A
As we know that Sum of all angles of a traingle = 180°
The ratio of angles of a triangle = 1 : 2 : 3.
∴ Sum of ratios = 1 + 2 + 3 = 6∴ Largest angle = 3 × 180° = 90° 6
∵ 180° = π radian∴ 90° = π × 90° = π radian 180 2

