If the internal bisectors of angles ∠ABC and ∠ACB

Home » Aptitude » Plane Geometry » Question

If the internal bisectors of angles ∠ABC and ∠ACB of ∆ABC intersect at point O, then ∠BOC = ?

1. 90° - ∠A
  2
2. 90° + ∠A
  2
3. 180° - ∠A
  2
4. 90° – ∠A

Correct Option: B

As per the given in question , we draw a figure a ∆ ABC and the internal bisectors of angles ∠ABC and ∠ACB intersect at point O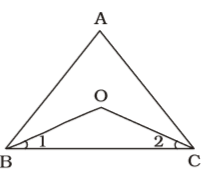

In ∆ BOC,
We know that sum of all three angles is 180°
∠1 + ∠2 + ∠BOC = 180° ...(i)
In ∆ ABC,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 2 ∠1 + 2 ∠2 = 180°

⇒	∠A	+ ∠1 + ∠2 = 90°
	2

⇒ ∠1 + ∠2 = 90° -	∠A
	2

From equation (i) ,

90° –	∠A	+ ∠BOC = 180°
	2

⇒ ∠BOC = 180° – 90° +	∠A	= 90° +	∠A
	2		2