Correct Option: C

On the basis of given question , we draw a figure of triangle PQR in which PS is the internal bisector of∠QPR and PT ⊥ QR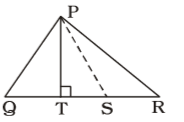

PS, is bisector of ∠QPR.
∴ ∠QPS = ∠SPR .....(i)
In ∆
PQT, ∠PQT + ∠PTQ + ∠QPT = 180°
⇒ ∠PQT + 90° + ∠QPT = 180°
⇒ ∠PQT + ∠QPT = 90°
⇒ ∠PQT = 90° – ∠QPT
⇒ ∠Q = 90° – ∠QPT .....(ii)
In ∆ PTR,
∠PRT + ∠TPR + ∠PTR = 180°
⇒ ∠PRT + ∠TPR + 90° = 180°
⇒ ∠PRT + ∠TPR = 90°
⇒ ∠PRT = 90° – ∠TPR ....(iii)
By equation (ii) – (iii),
∠Q – ∠R = (90° – ∠QPT) – (90° – ∠TPR)
⇒ ∠Q – ∠R = ∠TPR – ∠QPT
⇒ ∠Q – ∠R = (∠TPS + ∠SPR) – (∠QPS – ∠TPS)
⇒ ∠Q – ∠R = 2 ∠TPS