Plane Geometry
- Two circles touch each other externally at P. AB is a direct common tangent to the two circles, A and B are point of contact and ∠ PAB = 35°. Then ∠ ABP is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of two circles touch each other externally at P ,
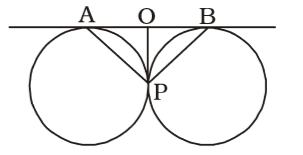
OA = OP
⇒ ∠PAB = ∠OPA = 35°
∴ ∠AOP = 110° ⇒ ∠POB = 70°Correct Option: B
As per the given in question , we draw a figure of two circles touch each other externally at P ,

OA = OP
⇒ ∠PAB = ∠OPA = 35°
∴ ∠AOP = 110° ⇒ ∠POB = 70°∴ ∠ABP = 180° - 70° = 110° = 55° 2 2
- PR is tangent to a circle, with centre O and radius 4 cm, at point Q. If ∠POR = 90°,OR = 5 cm and OP = 20/3 cm, then (in cm) the length of PR is :
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,

Given that , ∠POR = 90°,OR = 5 cm and OP = 20 cm. 3
OQ ⊥ PR
∴ From ∆ OPQ,
PQ = √OP² - OQ²= √ 
20 
² - 4² 3 PQ = √ 400 - 16 9 PQ = √ 400 - 144 9 PQ = √ 256 9 PQ = 16 cm. 3
From ∆ OQR,
Correct Option: D
According to question , we draw a figure of a circle with centre O ,

Given that , ∠POR = 90°,OR = 5 cm and OP = 20 cm. 3
OQ ⊥ PR
∴ From ∆ OPQ,
PQ = √OP² - OQ²= √ 
20 
² - 4² 3 PQ = √ 400 - 16 9 PQ = √ 400 - 144 9 PQ = √ 256 9 PQ = 16 cm. 3
From ∆ OQR,
QR = √OR² - OQ²
QR = √5² - 4² = √25 - 16 = √9 = 3 cm∴ PR = PQ + QR = 16 + 3 = 25 cm 3 3
- Two circles touch each other externally at point A and PQ is a direct common tangent which touches the circles at P and Q respectively. Then ∠PAQ =
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of two circles touch each other externally at point A and PQ is a direct common tangent ,

AO is perpendicular to PQ.
OA = OP = OQ.Correct Option: B
According to question , we draw a figure of two circles touch each other externally at point A and PQ is a direct common tangent ,

AO is perpendicular to PQ.
OA = OP = OQ.
⇒ ∠OPA = ∠OAP = ∠OQA = ∠OAQ = 45°
∴ ∠PAQ = 90°
- The tangents at two points A and B on the circle with centre O intersects at P ; If in quadrilateral PAOB, ∠AOB: ∠APB = 5 : 1, then measure of ∠APB is :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a circle with centre O,

Given that , ∠AOB: ∠APB = 5 : 1,
From figure ,
∠ OAP = ∠ OBP = 90°
∠ AOB + ∠ APB = 180°Correct Option: A
As per the given in question , we draw a figure of a circle with centre O,

Given that , ∠AOB: ∠APB = 5 : 1,
From figure ,
∠ OAP = ∠ OBP = 90°
∠ AOB + ∠ APB = 180°
⇒ 5∠ APB + ∠ APB = 180°
⇒ 6 ∠ APB = 180°
⇒ ∠ APB = 30°
- AB is a chord to a circle and PAT is the tangent to the circle at A. If ∠BAT = 75° and ∠BAC = 45°, C being a point on the circle, then ∠ABC is equal to
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a circle with centre O ,

If a line touches a circle and from the point of contact a chord is drawn, the angles which this chord makes with the given line are equal respe ctively to the angles formed in the corresponding alternate segments.Correct Option: C
On the basis of question we draw a figure of a circle with centre O ,

If a line touches a circle and from the point of contact a chord is drawn, the angles which this chord makes with the given line are equal respe ctively to the angles formed in the corresponding alternate segments.
∴ ∠ACB = ∠BAT = 75° and ∠BAC = 45°
∠ABC = 180° – 45° – 75°= 60°

