Plane Geometry
- In a circle with centre at O (0, 0) and radius 5 cm, AB is a chord of length 8 cm. If OM is perpendicular to AB, then the length of OM is:
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a circle with centre O ,
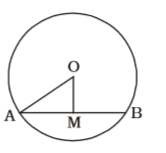
Given , AB = 8 cm
AM = MB = 4 cm
OA = 5 cm
From ∆ AOM ,
∴ OM = √OA² - AM²
OM = √5² - 4²Correct Option: B
On the basis of question we draw a figure of a circle with centre O ,

Given , AB = 8 cm
AM = MB = 4 cm
OA = 5 cm
From ∆ AOM ,
∴ OM = √OA² - AM²
OM = √5² - 4²
OM = √25 - 16
OM = √9 = 3 cm
- AB is the diameter of a circle with centre O. P be a point on it. If ∠POA = 120°. Then, ∠PBO = ?
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,
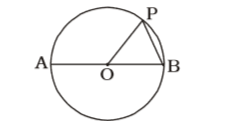
∠AOB = 180°
∠AOP = 120°
we know that , ∠AOP + ∠POB = 180°
∴ ∠POB = 180° – 120° = 60°
OP = OB = radiiCorrect Option: A
According to question , we draw a figure of a circle with centre O ,

∠AOB = 180°
∠AOP = 120°
we know that , ∠AOP + ∠POB = 180°
∴ ∠POB = 180° – 120° = 60°
OP = OB = radii∴ ∠OPB = ∠PBO = 120° = 60° 2
- In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a circle with centre O ,
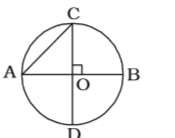
Radius = OA = OB = OC = AB 2
∴ AC = √OA² + OC²
From ∆ AOCAC = √ 
AB 
2 + 
AB 
2 2 2 AC = √ AB² + AB² 4
Correct Option: D
On the basis of question we draw a figure of a circle with centre O ,

Radius = OA = OB = OC = AB 2
∴ AC = √OA² + OC²
From ∆ AOCAC = √ 
AB 
2 + 
AB 
2 2 2 AC = √ AB² + AB² 4 AC = √ AB² 2 AC = AB √2
- AB and CD are two parallel chords of a circle lying on the opposite side of the centre and the distance between them is 17 cm. The length of AB and CD are 10 cm and 24 cm respectively. The radius (in cm) of the circle is :
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,
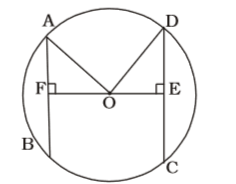
AB = 10 cm.
∴ AF = FB = 5 cm.
CD = 24 cm.
∴ CE = DE = 12 cm.
Let OE = y cm
∴ OF = (17 – y) cm
From ∆ ODE,
OD = √OE² + DE²
OD = √y² + 12² ..... (i)
From ∆ OAF,
OA = √OF² + AF²
OA = √(17 - y)² + 5² ..... (ii)
∵ OA = OD
∴ √y² + 12² = √(17 - y)² + 5²
⇒ y² + 144 = 289 – 34y + y² + 25
⇒ 34y = 289 + 25 – 144 = 170⇒ y = 170 = 5 34
Correct Option: A
According to question , we draw a figure of a circle with centre O ,

AB = 10 cm.
∴ AF = FB = 5 cm.
CD = 24 cm.
∴ CE = DE = 12 cm.
Let OE = y cm
∴ OF = (17 – y) cm
From ∆ ODE,
OD = √OE² + DE²
OD = √y² + 12² ..... (i)
From ∆ OAF,
OA = √OF² + AF²
OA = √(17 - y)² + 5² ..... (ii)
∵ OA = OD
∴ √y² + 12² = √(17 - y)² + 5²
⇒ y² + 144 = 289 – 34y + y² + 25
⇒ 34y = 289 + 25 – 144 = 170⇒ y = 170 = 5 34
∴ From equation (i),
OD = √y² + 12² = √5² + 144
OD = √169 = 13 cm.
- Two chords of length a unit and b unit of a circle make angles 60° and 90° at the centre of a circle respectively, then the correct relation is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of circle with centre O in which two chords of length a unit and b unit ,

radius(r) = OA = OB = OC = OD
∠OAB = 90°; AB = b, CD = a
From ∆ OAB,
OA² + OB² = AB²
⇒ r² + r² = b²
⇒ 2r² = b²⇒ r² = b² 2 ⇒ r = b .......(ii) √2
In ∆ OCD,
∠COD = 60° ;
Correct Option: B
As per the given in question , we draw a figure of circle with centre O in which two chords of length a unit and b unit ,

radius(r) = OA = OB = OC = OD
∠OAB = 90°; AB = b, CD = a
From ∆ OAB,
OA² + OB² = AB²
⇒ r² + r² = b²
⇒ 2r² = b²⇒ r² = b² 2 ⇒ r = b .......(ii) √2
In ∆ OCD,
∠COD = 60° ;
∴ ∠OCD = ∠ODC = 60°
∴ OC = CD
⇒ r = a ......(ii)
From equations (i) and (ii),b = a ⇒ b = √2a √2

