Plane Geometry
- In a triangle ABC, ∠A = 70°, ∠B = 80° and D is the incentre of ∆ ABC. ∠ACB = 2x° and ∠BDC = y°. The values of x and y, respectively are
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure triangle ABC whose D is the incentre ,

The point of intersection of internal bisectors of angles of a triangle is in-centre.
∠A = 70°; ∠B = 80°
∴ ∠C = 180° – (70° + 80°) = 30°
∴ ∠ACB = 2x° = 30° ⇒ x = 15°∠BDC = 180° - ∠B - ∠C 2 2
Correct Option: B
As per the given in question , we draw a figure triangle ABC whose D is the incentre ,

The point of intersection of internal bisectors of angles of a triangle is in-centre.
∠A = 70°; ∠B = 80°
∴ ∠C = 180° – (70° + 80°) = 30°
∴ ∠ACB = 2x° = 30° ⇒ x = 15°∠BDC = 180° - ∠B - ∠C 2 2 ∠BDC = 180° - 80° - 30° 2 2
∠BDC = 180° – 40° – 15° = 125° = y
- If O is the orthocentre of a triangle ABC and ∠BOC = 100°, the measure of ∠BAC is
-
View Hint View Answer Discuss in Forum
We draw a figure triangle ABC whose O is the orthocentre ,

Given , ∠BOC = 180°
∠BOC = 100° – ∠ACorrect Option: C
We draw a figure triangle ABC whose O is the orthocentre ,

Given , ∠BOC = 180°
∠BOC = 100° – ∠A
⇒ ∠A = 180° – ∠BOC
∠A = 180° – 100° = 80°
- Two medians AD and BE of ∆ ABC intersect at G at right angles. If AD = 9 cm and BE = 6 cm, then the length of BD (in cm) is
-
View Hint View Answer Discuss in Forum
We draw a figure triangle ABC in which two medians AD and BE intersect at G at right angles ,
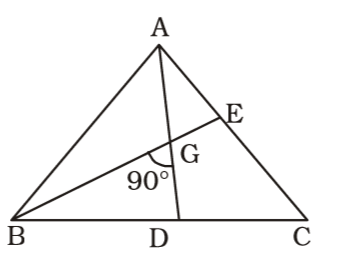
AD = 9 cm.⇒ GD = 1 × 9 = 3cm 3
BE = 6 cm
Correct Option: C
We draw a figure triangle ABC in which two medians AD and BE intersect at G at right angles ,

AD = 9 cm.⇒ GD = 1 × 9 = 3cm 3
BE = 6 cm⇒ BG = 2 × 6 = 4 cm 3
∴ BD = √3² + 4² = √9 + 16 = 5 cm.
- If the length of the three sides of a triangle are 6 cm, 8 cm and 10 cm, then the length of the median to its greatest side is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure triangle ABC
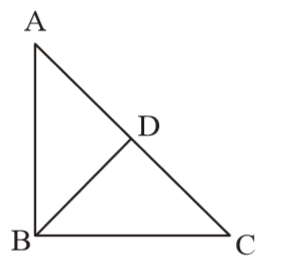
Here, 6² + 8² = 10²
∴ ∆ ABC is a right angled triangle.
AC = 10 cm
Point D is the mid-point of side BC.Correct Option: C
As per the given in question , we draw a figure triangle ABC

Here, 6² + 8² = 10²
∴ ∆ ABC is a right angled triangle.
AC = 10 cm
Point D is the mid-point of side BC.
Point D is equidistant from the vertices A, B and C.
∴ AD = BD = CD = 5 cm
- The length of the three sides of a right angled triangle are (x –2) cm, x cm and (x + 2) cm respectively. Then the value of x is
-
View Hint View Answer Discuss in Forum
According to question ,
In a right angled triangle,
(Hypotenuse)² = (Perpendicular)² + (Base)²
⇒ (x + 2)² = (x – 2)² + x²
⇒ x² + 4x + 4 = x² – 4x + 4 + x²
⇒ x² – 8x = 0Correct Option: B
According to question ,
In a right angled triangle,
(Hypotenuse)² = (Perpendicular)² + (Base)²
⇒ (x + 2)² = (x – 2)² + x²
⇒ x² + 4x + 4 = x² – 4x + 4 + x²
⇒ x² – 8x = 0
⇒ x (x – 8) = 0
⇒ x = 8

