Plane Geometry
- In ∆ ABC, ∠A + ∠B = 145° and ∠C + 2∠B = 180°. State which one of the following relations is true ?
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a triangle ABC

Given , ∠A + ∠B = 145°
∠C = 180° – 145° = 35°
∠C + 2∠B = 180°
⇒ 2∠B = 180° – 35° = 145°⇒ ∠B = 145° 2
Correct Option: D
According to question , we draw a figure of a triangle ABC

Given , ∠A + ∠B = 145°
∠C = 180° – 145° = 35°
∠C + 2∠B = 180°
⇒ 2∠B = 180° – 35° = 145°⇒ ∠B = 145° 2
⇒ 72.5° = ∠A
⇒ ∠B > ∠C
∴ AC > AB
- In a triangle ABC, BC is produced to D so that CD = AC. If ∠BAD = 111° and ∠ACB = 80°, then the measure of ∠ABC is :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a triangle ABC in which BC is produced to D so that CD = AC

Given , ∠BAD = 111° and ∠ACB = 80°
∴ ∠ACD = 180° – 80° = 100°
∠CAD = ∠CDA [CD = AC]Correct Option: D
As per the given in question , we draw a figure of a triangle ABC in which BC is produced to D so that CD = AC

Given , ∠BAD = 111° and ∠ACB = 80°
∴ ∠ACD = 180° – 80° = 100°
∠CAD = ∠CDA [CD = AC]∠CAD = 80° = 40° 2
∠BAC = 111° – 40° = 71°
∠ABC = 180° – 71° – 80° = 29°
- In the following figure, AB be diameter of a circle whose centre is O. If ∠AOE = 150°, ∠DAO = 51° then the measure of ∠CBE is :
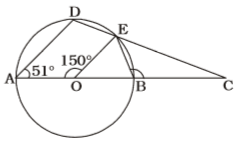
-
View Hint View Answer Discuss in Forum
According to given figure in question ,

Given , ∠AOE = 150°, ∠DAO = 51°
∴ ∠EOB + ∠AOE = 180°
∠EOB = 180° – 150° = 30°
OE = OBCorrect Option: C
According to given figure in question ,

Given , ∠AOE = 150°, ∠DAO = 51°
∴ ∠EOB + ∠AOE = 180°
∠EOB = 180° – 150° = 30°
OE = OB
∴ ∠OEB = ∠OBE = 150 ÷ 2 = 75°
∴ ∠CBE = 180° – 75° = 105°
- If O be the circumcentre of a triangle PQR and ∠QOR = 110°, ∠OPR = 25°, then the measure of ∠PRQ is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a triangle PQR with circumcentre O

Given , ∠QOR = 110°
∠OPR = 25°
∴ ∠QPR = 110° ÷ 2 = 55°
OR = OP
∴ ∠OPR = ∠PRO = 25°Correct Option: D
As per the given in question , we draw a figure of a triangle PQR with circumcentre O

Given , ∠QOR = 110°
∠OPR = 25°
∴ ∠QPR = 110° ÷ 2 = 55°
OR = OP
∴ ∠OPR = ∠PRO = 25°
∴ ∠OQR = ∠ORQ = 70 ÷ 2 = 35°
∴ ∠PRQ = 25° + 35° = 60°
- In a triangle ABC, ∠A = 90°, ∠C = 55°, AD x BC. What is the value of ∠BAD ?
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a triangle ABC

Here , ∠A = 90°, ∠C = 55°,
∴ ∠B + ∠C = 90°
∴ ∠B = 90° – 55° = 35°Correct Option: D
As per the given in question , we draw a figure of a triangle ABC

Here , ∠A = 90°, ∠C = 55°,
∴ ∠B + ∠C = 90°
∴ ∠B = 90° – 55° = 35°
∠ADB = 90°
∴ ∠BAD = 90° – 35° = 55°

