Plane Geometry
- Two chords of lengths a metre and b metre subtend angles 60° and 90° at the centre of the circle respectively. Which of the following is true ?
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure a circle two chords of lengths a metre and b metre subtend angles 60° and 90° at the centre O ,
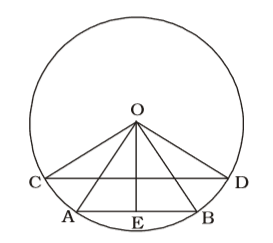
Radius of circle = r units
In ∆ OCD, ∠COD = 90°
∴ CD² = OC² + OD²
⇒ b² = r² + r² = 2r² ...(i)
In ∆ OAB,
OE ⊥ AB
∠OAB = 60°AE = a 2 ∴ cos60° = AE OA ⇒ = a 1 2 2 r
Correct Option: A
As per the given in question , we draw a figure a circle two chords of lengths a metre and b metre subtend angles 60° and 90° at the centre O ,

Radius of circle = r units
In ∆ OCD, ∠COD = 90°
∴ CD² = OC² + OD²
⇒ b² = r² + r² = 2r² ...(i)
In ∆ OAB,
OE ⊥ AB
∠OAB = 60°AE = a 2 ∴ cos60° = AE OA ⇒ = a 1 2 2 r ⇒ 1 = a ⇒ a = r........(ii) 2 2r
From equations (i) and (ii),
b² = 2a²
⇒ b = √2a
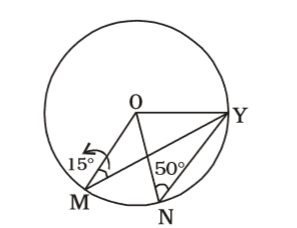
- In the given figure, ∠ONY = 50° and ∠OMY = 15°. Then the value of the ∠MON is
-
View Hint View Answer Discuss in Forum
According to question ,
In ∆ ONY, ON = OY = radii
∠ONY = 50° = ∠OYN
∴ ∠NOY = 180° – 2 × 50° = 80°
In ∆ OMY,
OM = OY = radiiCorrect Option: D
According to question ,

In ∆ ONY, ON = OY = radii
∠ONY = 50° = ∠OYN
∴ ∠NOY = 180° – 2 × 50° = 80°
In ∆ OMY,
OM = OY = radii
∴ ∠OMY = ∠OYN = 15°
∴ ∠MOY = 180° – 2 × 15° = 150°
∴ ∠MON = 150° – 80° = 70°
- A, B, C are three points on the circumference of a circle and if AB = AC = 5√2 cm and ∠BAC = 90°, find the radius.
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure a circle in which A, B, C are three points on the circumference ,

In ∆s OAB and OCA,
OC = OA = OB = radii
2 ∠ OAB + ∠ AOB = 180°
2 ∠ OAC + ∠ AOC = 180°
∴ ∠ AOB + ∠ AOC = 360° – 2 (∠ OAB + ∠ OAC)
∠ AOB + ∠ AOC = 360° – 2 × 90° = 180°
AB = AC
∴ ∠ AOB = 90°
∠ OAB = 45°⇒ sin OAB = OB AB
Correct Option: B
As per the given in question , we draw a figure a circle in which A, B, C are three points on the circumference ,

In ∆s OAB and OCA,
OC = OA = OB = radii
2 ∠ OAB + ∠ AOB = 180°
2 ∠ OAC + ∠ AOC = 180°
∴ ∠ AOB + ∠ AOC = 360° – 2 (∠ OAB + ∠ OAC)
∠ AOB + ∠ AOC = 360° – 2 × 90° = 180°
AB = AC
∴ ∠ AOB = 90°
∠ OAB = 45°⇒ sin OAB = OB AB ⇒ sin 45° = OB 5√2
⇒ OB = 5 √2.sin 45°OB = 5 √2 × 1 = 5cm. √2
- In ∆ABC, ∠ABC = 70°, ∠BCA = 40°. O is the point of intersection of the perpendicular bisectors of the sides, then the angle ∠BOC is
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of ∆ABC ,

Given that , ∠ABC = 70°, ∠BCA = 40°
OA = OB = OC = Circum-radius
In ∆ ABC,
∠A = 180° – 70° – 40° = 180° – 110° = 70°Correct Option: D
On the basis of question we draw a figure of ∆ABC ,

Given that , ∠ABC = 70°, ∠BCA = 40°
OA = OB = OC = Circum-radius
In ∆ ABC,
∠A = 180° – 70° – 40° = 180° – 110° = 70°
The angle subtended by an arc at the centre is twice to that at the circumference.
∴ ∠BOC = 2∠BAC
∠BOC = 2 × 70 = 140°
- ‘O’ is the centre of the circle, AB is a chord of the circle, OM ⊥ AB. If AB = 20 cm, OM = 2 11 cm, then radius of the cir-cle is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,
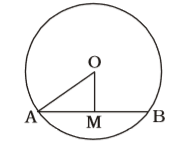
AB = 20 cm.
AM = MB = 10 cm.
From ∆ AOM ,
OM = 2 √11 cm.
∴ Radius OA = √OM² + AM²
OA = √(2√11)² + 10²
OA = √4 × 11 + 100Correct Option: B
According to question , we draw a figure of a circle with centre O ,

AB = 20 cm.
AM = MB = 10 cm.
From ∆ AOM ,
OM = 2 √11 cm.
∴ Radius OA = √OM² + AM²
OA = √(2√11)² + 10²
OA = √4 × 11 + 100
OA = √44 + 100
OA = √144 = 12 cm.

