As per the given in question , we draw a figure parallelogram PQRS

we know that , ∠SPQ + ∠PQR = 180°
⇒ 4 ∠PQR + ∠PQR = 180°
⇒ 5 ∠PQR = 180°

Correct Option: A

As per the given in question , we draw a figure parallelogram PQRS

we know that , ∠SPQ + ∠PQR = 180°
⇒ 4 ∠PQR + ∠PQR = 180°
⇒ 5 ∠PQR = 180°

According to question , we draw a figure of cyclic parallelogram ABCD

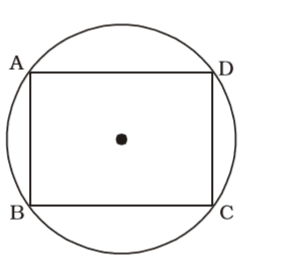
Here , ∠ = 70°,
∴ ∠B + ∠D = 180°

Correct Option: D

According to question , we draw a figure of cyclic parallelogram ABCD

Here , ∠ = 70°,
∴ ∠B + ∠D = 180°
⇒ 2∠B = 180°
⇒ ∠B = 90°

On the basis of question we draw a figure of cyclic trapezium ABCD

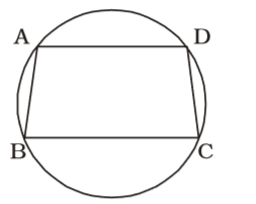
Given , ∠ABC = 70°
∠ABC + ∠CDA = 180°

Correct Option: B

On the basis of question we draw a figure of cyclic trapezium ABCD

Given , ∠ABC = 70°
∠ABC + ∠CDA = 180°
⇒ ∠CDA = 180° – 70° = 110°
∴ ∠BCD = 180° – 110° = 70°

On the basis of question we draw a figure of cyclic trapezium ABCD whose sides AD and BC are parallel to each other ,

∠ABC + ∠CDA = 180°
⇒ ∠CDA = 180° – 72° = 108°

Correct Option: D

On the basis of question we draw a figure of cyclic trapezium ABCD whose sides AD and BC are parallel to each other ,

∠ABC + ∠CDA = 180°
⇒ ∠CDA = 180° – 72° = 108°
AD || BC
∠BCD = ∠ADE = ∠ABC = 72°

According to question , we draw a figure of cyclic quadrilateral ABCD

Given , an exterior angle of a cyclic quadrilateral = 50°
From figure ,
As we know that , ∠ABC + ∠ADC = 180°
∠CBE = 50°

Correct Option: C

According to question , we draw a figure of cyclic quadrilateral ABCD

Given , an exterior angle of a cyclic quadrilateral = 50°
From figure ,
As we know that , ∠ABC + ∠ADC = 180°
∠CBE = 50°
∴ ∠ABC = 180° – 50° = 130°
∴ ∠ADC = 180° – 130° = 50°