Plane Geometry
- The point equidistant from the sides of a triangle is called
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of equilateral triangle ,
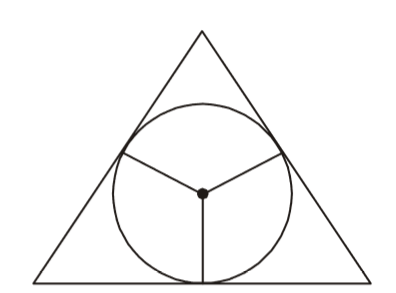
The point equidistant from the sides of a triangle is called Incentre .Correct Option: B
On the basis of question we draw a figure of equilateral triangle ,

The point equidistant from the sides of a triangle is called Incentre .
Or The point of intersection of the internal bisectors of the angles of a triangle meet at a point that is incentre-equidistant from the sides.
- In ∆ ABC and ∆ DEF, if ∠A = 50°, ∠B = 70°, ∠C = 60°, ∠D = 60°, ∠E = 70° and ∠F = 50°, then
-
View Hint View Answer Discuss in Forum
According to question ,
In ∆ ABC and ∆ DEF,
∠A = ∠F = 50°
∠B = ∠E = 70°
∠C = ∠D = 60°Correct Option: A
According to question ,
In ∆ ABC and ∆ DEF,
∠A = ∠F = 50°
∠B = ∠E = 70°
∠C = ∠D = 60°
∴ ∆ ABC ~ ∆ FED
- In a ∆ABC, if 4∠A = 3 ∠B = 12 ∠C, find ∠A.
-
View Hint View Answer Discuss in Forum
As per the given in question ,
∴ 4∠A = 3∠B = 12∠C
{ LCM of 4 , 3 , 12 is 12 }⇒ 4∠A = 3∠B = 12∠C 12 12 12 ⇒ ∠A = ∠B = ∠C 3 4 1
∴ ∠A : ∠B : ∠C = 3 : 4 : 1;
∠A + ∠B + ∠C = 180°
∴ Sum of the terms of ratio = 3 + 4 + 1 = 8
Correct Option: C
As per the given in question ,
∴ 4∠A = 3∠B = 12∠C
{ LCM of 4 , 3 , 12 is 12 }⇒ 4∠A = 3∠B = 12∠C 12 12 12 ⇒ ∠A = ∠B = ∠C 3 4 1
∴ ∠A : ∠B : ∠C = 3 : 4 : 1;
∠A + ∠B + ∠C = 180°
∴ Sum of the terms of ratio = 3 + 4 + 1 = 8∴ ∠A = 3 × 180° = 67.5° 8
- In triangle ABC, ∠BAC = 90° and AD is perpendicular to BC. If AD = 6 cm and BD = 4 cm, then the length of BC is :
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure triangle ABC in which AD is perpendicular to BC
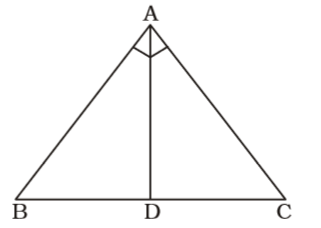
Given , AD = 6 cm. and BD = 4 cm.
∴ AB = √AD² + BD²
AB = √6² + 4²
AB = √36 + 16
AB = √52 cm.⇒ BD = AB² ⇒ 4 = 52 BC BC
Correct Option: C
According to question , we draw a figure triangle ABC in which AD is perpendicular to BC

Given , AD = 6 cm. and BD = 4 cm.
∴ AB = √AD² + BD²
AB = √6² + 4²
AB = √36 + 16
AB = √52 cm.⇒ BD = AB² ⇒ 4 = 52 BC BC ⇒ BC = 52 = 13 cm. 4
- D and E are the points on the sides AB and AC respectively of a ∆ ABC and AD = 8 cm, DB = 12 cm, AE = 6 cm and EC = 9 cm, then BC is equal to :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure triangle ABC whose D and E are the points on the sides AB and AC respectively
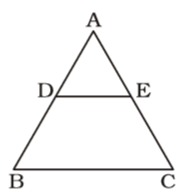
Here , AD = 8 cm, DB = 12 cm, AE = 6 cm and EC = 9 cm
According to the question,AD = 8 = 2 DB 12 3 AE = 6 = 2 EC 9 3 ∴ AD = AE = 2 DB EC 3 ⇒ DB = EC = 3 AD AE 2
Correct Option: B
As per the given in question , we draw a figure triangle ABC whose D and E are the points on the sides AB and AC respectively

Here , AD = 8 cm, DB = 12 cm, AE = 6 cm and EC = 9 cm
According to the question,AD = 8 = 2 DB 12 3 AE = 6 = 2 EC 9 3 ∴ AD = AE = 2 DB EC 3 ⇒ DB = EC = 3 AD AE 2 ⇒ DB + AD = 3 + 2 = EC + AE AD 2 AE ⇒ AB = 5 = AC AD 2 AE
∴ ∆ ABC ~ ∆ ADE∴ AB = BC = 5 AD DE 2 ⇒ BC = 5 DE 2

