Plane Geometry
- In ∆ ABC, a line parallel to BC intersects AB and AC at D and E. If AE = 3 AD, find the ratio BD : EC.
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a triangle ABC and a line parallel to BC intersects AB and AC at D and E
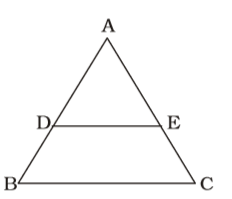
In ∆ ADE and ∆ ABC,
∠D = ∠B; ∠E = ∠C
∠A = ∠A
∴ Both triangles are similar.
As we know that ,∴ AD = AE AB AC ⇒ AB = AC AD AE ⇒ AB - 1 = AC - 1 AD AE
Correct Option: A
According to question , we draw a figure of a triangle ABC and a line parallel to BC intersects AB and AC at D and E

In ∆ ADE and ∆ ABC,
∠D = ∠B; ∠E = ∠C
∠A = ∠A
∴ Both triangles are similar.
As we know that ,∴ AD = AE AB AC ⇒ AB = AC AD AE ⇒ AB - 1 = AC - 1 AD AE ⇒ BD = EC AD AE ⇒ BD = AD = 1 EC AE 3
- In ∆ ABC, AB = 6 cms, BC = 10 cms, AC = 8cm and AD ⊥ BC. Find the value of the ratio of BD : DC.
-
View Hint View Answer Discuss in Forum
As per the given question , we draw a figure of right angled triangle CAB

Here , AB = 6 cms, BC = 10 cms, AC = 8cm and AD ⊥ BC
6² + 8² = 10²
∴ ∆ ABC is a right angled triangle.∆ ABC = 1 × Base × Height 2 ∴ 1 × AB × BC = 1 × BC × AD 2 2
⇒ 6 × 8 = 10 × AD⇒ AD = 24 cm. 5
Let BD = y cm.
From ∆ ABD,BD = √6² - 
24 
² 5 BD = √36 - 576 = √ 900 - 576 25 25 BD = √ 324 = 18 cm. 25 5
Correct Option: B
As per the given question , we draw a figure of right angled triangle CAB

Here , AB = 6 cms, BC = 10 cms, AC = 8cm and AD ⊥ BC
6² + 8² = 10²
∴ ∆ ABC is a right angled triangle.∆ ABC = 1 × Base × Height 2 ∴ 1 × AB × BC = 1 × BC × AD 2 2
⇒ 6 × 8 = 10 × AD⇒ AD = 24 cm. 5
Let BD = y cm.
From ∆ ABD,BD = √6² - 
24 
² 5 BD = √36 - 576 = √ 900 - 576 25 25 BD = √ 324 = 18 cm. 25 5 ∴ CD = 10 - 18 = 32 cm. 5 5 ∴ BD : CD = 18 : 32 = 9 : 16 5 5
- Two chords AB and CD of a circle with centre O intersect at point P within the circle. ∠AOC + ∠BOD = ?
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O in which two chords AB and CD intersect at point P within the circle
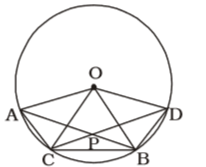
Arc AC subtends ∠AOC at the centre.
∠AOC = 2∠ABC
Similarly, ∠BOD = 2∠BCDCorrect Option: B
According to question , we draw a figure of a circle with centre O in which two chords AB and CD intersect at point P within the circle

Arc AC subtends ∠AOC at the centre.
∠AOC = 2∠ABC
Similarly, ∠BOD = 2∠BCD
On adding, we get
∠AOC + ∠BOD = 2(∠ABC + ∠BCD) = 2∠APC [∵ ∠APC is the exterior angle]
- PQRS is a cyclic quadrilateral. The bisectors of the angles ∠P and ∠R meet the circle ABCD at A and B respectively. If the radius of the circle be r units, then AB = ?
-
View Hint View Answer Discuss in Forum
As per the above given question , we draw a figure of a cyclic quadrilateral PQRS and the bisectors of the angles ∠P and ∠R meet the circle ABCD at A and B respectively
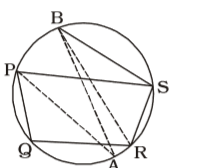
PQRS is a cyclic quadrilateral.
∠P + ∠R = 180°⇒ 1 ∠P + 1 ∠R = 90° 2 2
⇒ ∠APS + ∠BRS = 90° ....(i)
Correct Option: B
As per the above given question , we draw a figure of a cyclic quadrilateral PQRS and the bisectors of the angles ∠P and ∠R meet the circle ABCD at A and B respectively

PQRS is a cyclic quadrilateral.
∠P + ∠R = 180°⇒ 1 ∠P + 1 ∠R = 90° 2 2
⇒ ∠APS + ∠BRS = 90° ....(i)
But ∠BRS and ∠BPS are angles in the same segment with chord BS.
∴ ∠BRS = ∠BPS .....(ii)
∴ ∠APS + ∠BPS = 90°
⇒ ∠APB = 90°
∴ AB is the diameter.
- A triangle ABC is inscribed in a circle and the bisectors of the angles A, B and C meet the circumference at P, Q and R respectively. The angles of the triangle PQR respectively are
-
View Hint View Answer Discuss in Forum
On the basis of given question , we draw a figure of a triangle ABC inscribed in a circle and the bisectors of the angles A, B and C meet the circumference at P, Q and R respectively
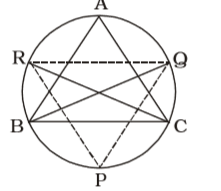
∠BQP = ∠BAP∠BQP = ∠A 2
∠BQR = ∠BCR∠BQR = 1 ∠C 2 ∴ ∠PQR = 1 (∠A + ∠C) 2 ∴ ∠PQR = 1 (180° - ∠B) = 90° - ∠B 2 2
∠APR = ∠ACR∴ ∠PQR = 1 ∠C 2
Also,∠APR = ∠ABQ⇒ ∠APR = 1 ∠B 2
Correct Option: C
On the basis of given question , we draw a figure of a triangle ABC inscribed in a circle and the bisectors of the angles A, B and C meet the circumference at P, Q and R respectively

∠BQP = ∠BAP∠BQP = ∠A 2
∠BQR = ∠BCR∠BQR = 1 ∠C 2 ∴ ∠PQR = 1 (∠A + ∠C) 2 ∴ ∠PQR = 1 (180° - ∠B) = 90° - ∠B 2 2
∠APR = ∠ACR∴ ∠PQR = 1 ∠C 2
Also,∠APR = ∠ABQ⇒ ∠APR = 1 ∠B 2 ∴ ∠APQ + ∠APR = 1 (∠B + ∠C) 2 ⇒ ∠QPR = 1 (180° - ∠A) = 90° - ∠A 2 2
Similarly,∠QRP = 90 - ∠C 2

