A triangle ABC is inscribed in a circle and the bisectors

Home » Aptitude » Plane Geometry » Question

A triangle ABC is inscribed in a circle and the bisectors of the angles A, B and C meet the circumference at P, Q and R respectively. The angles of the triangle PQR respectively are

1. 90° - A , 90° + A , 90° + C
  2 2 2
2. 90° + A , 90° - B , 90° - C
  2 2
3. 90° - A , 90° - B , 90° - C
  2 2 2
4. None of these

Correct Option: C

On the basis of given question , we draw a figure of a triangle ABC inscribed in a circle and the bisectors of the angles A, B and C meet the circumference at P, Q and R respectively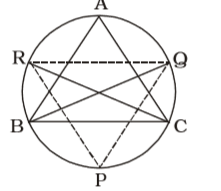

∠BQP = ∠BAP

∠BQP =	∠A
	2

∠BQR = ∠BCR

∠BQR =	1	∠C
	2

∴ ∠PQR =	1	(∠A + ∠C)
	2

∴ ∠PQR =	1	(180° - ∠B) = 90° -	∠B
	2		2

∠APR = ∠ACR

∴ ∠PQR =	1	∠C
	2

Also,∠APR = ∠ABQ

⇒ ∠APR =	1	∠B
	2

∴ ∠APQ + ∠APR =	1	(∠B + ∠C)
	2

⇒ ∠QPR =	1	(180° - ∠A) = 90° -	∠A
	2		2

Similarly,

∠QRP = 90 -	∠C
	2